| Line 1: | Line 1: | ||
| − | [[Category:PMOR benchmark, linear, two geometrical parameters, second order system]] |
+ | [[Category:PMOR benchmark, linear, time invariant, two geometrical parameters, second order system]] |
==Description of the device== |
==Description of the device== |
||
Revision as of 09:34, 21 November 2011
Description of the device
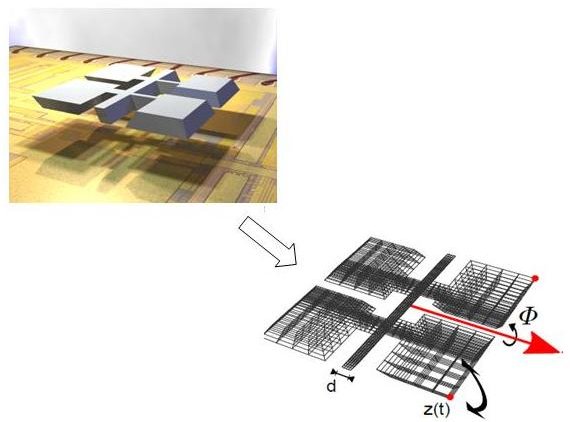
The device is a MEMS gyroscope based on the butterfly gyroscope [1] developed at the Imego institute in Gothenburg, Sweden (see also: http://simulation.uni-freiburg.de/downloads/benchmark/The Butterfly Gyro (35889)). A gyroscope is a device used to measure angular rates in up to three axes.
The basic working principle of the gyroscope can be described as follows [2]. Without applied external rotation, the paddles vibrate in phase with the function z(t). Under the influence of an external rotation about the x-axis (drawn in red), an additional force due to the Coriolis acceleration acts upon the paddles. This force leads to an additional small out-of-phase vibration between two paddles on the same side of the bearing. This out-of phase vibration is measured as the difference of the z-displacement of the nodes with the red dots. Thus, measuring the displacement of two adjacent paddles, the rotation velocity can be ascertained.
Motivation of MOR
When planning for and making decisions on future improvements of the Butterfly Gyroscope, it is of importance to improve the efficiency of the gyro simulations. Repeated analysis of the sensor structure have to be conducted with respect to a number of important issues. Examples of such are sensitivity to shock, linear and angular vibration sensitivity, reaction to large rates and/or acceleration, different types of excitation load cases and the effect of force-feedback. The use of model order reduction indeed decreases run time for repeated simulations.
Description of the parametrized model
Two parameters are of special interest for the model. The first one is the
quantity that is to be sensed, the rotation velocity around the  -axes.
The second parameter is the width of the bearing, d.
The parametrized system below is obtained by
finite element discretization of the parametrized model (in the form of partial differential equations) for the gyroscope. (The details of constructing the parametrized system can be found in [2]. The system is of the following
form:
-axes.
The second parameter is the width of the bearing, d.
The parametrized system below is obtained by
finite element discretization of the parametrized model (in the form of partial differential equations) for the gyroscope. (The details of constructing the parametrized system can be found in [2]. The system is of the following
form:
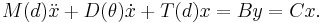
Here,
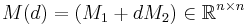 is the mass matrix,
is the mass matrix,
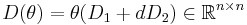 is the damping matrix,
is the damping matrix,
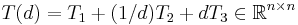 is the stiffness matrix,
is the stiffness matrix,
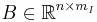 is the load vector,
is the load vector, 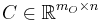 is the output matrix,
is the output matrix, 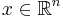 is the state vector, and
is the state vector, and 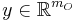 is the output response.
is the output response.
The variables 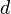 and
and 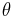 are the parameters of the system, where
are the parameters of the system, where
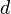 is the width of the
bearing and
is the width of the
bearing and 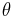 is the rotation velocity along the
is the rotation velocity along the  -axis.
-axis.
The interesting output 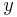 of the system is
of the system is 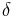 which is the
difference of the displacement
which is the
difference of the displacement 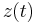 between the two red dots on
the same side of the bearing (see Fig.1). The number of degrees of freedom is
between the two red dots on
the same side of the bearing (see Fig.1). The number of degrees of freedom is 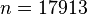 .
.
The interesting range for the parameters are: ![\theta\in [10^{-7}, 10^{-5}]](/morwiki/images/math/c/7/b/c7b0efa19e225aa5e038426cd80c3295.png) and
and ![d\in [1,2]](/morwiki/images/math/2/4/4/244c3333a4e36be25805ee4d952a245e.png) . The device works in the frequency range
. The device works in the frequency range ![f\in [0.025, 0.25]](/morwiki/images/math/8/f/1/8f1b9fd6143653e37abb4aeea17e1673.png) MHz. Typical values of the damping variables
MHz. Typical values of the damping variables 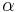 and
and 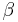 are
are 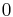 and
and 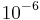 , respectively. It has been proven by Salimbahrami [3] that the matrices associated with the damping variables do not have to be taken into account during the process of model reduction.
, respectively. It has been proven by Salimbahrami [3] that the matrices associated with the damping variables do not have to be taken into account during the process of model reduction.
Data information
The systems matrices 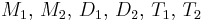 , and
, and 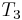 are in the MatrixMarket format (http://math.nist.gov/MatrixMarket/), and can be downloaded here File:Matrices.tgz.
are in the MatrixMarket format (http://math.nist.gov/MatrixMarket/), and can be downloaded here File:Matrices.tgz. 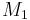 corresponds to the file Bmass1.dat,
corresponds to the file Bmass1.dat, 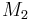 corresponds to the file Bmass2.dat.,
corresponds to the file Bmass2.dat., 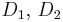 correspond to the files Bdamp1.dat, Bdamp2.dat, respectively.
correspond to the files Bdamp1.dat, Bdamp2.dat, respectively.  correspond to the files Bstiff1.dat, Bstiff2.dat, Bstiff3.dat, respectively.
The load vector
correspond to the files Bstiff1.dat, Bstiff2.dat, Bstiff3.dat, respectively.
The load vector  can be obtained from the file Bload.dat.
can be obtained from the file Bload.dat.
References
[1] J. Lienemann, D. Billger, E. B. Rudnyi, A. Greiner, J. G. Korvink, "MEMS Compact Modeling Meets Model Order Reduction: Examples of the Application of Arnoldi Methods to Microsystem Devices," Nanotech, 2004, pp. 303–306.
[2] C. Moosmann, "ParaMOR---- Model Order Reduction for parameterized MEMS applications," PhD thesis, Department of Microsystems Engineering, University of Freiburg, 2007.
[3] B. Salimbahrami, R. Eid, B. Lohmann, "Model Reduction by Second Order Krylov Subspaces: Extensions, Stability and Proportional Damping," IEEE International Symposium on Intelligent Control, 2006, pp. 2997–3002.