(→Plots) |
|||
| Line 132: | Line 132: | ||
Contact information: |
Contact information: |
||
| − | '' [[User: |
+ | '' [[User:Ionita]] 14:38, 29 November 2011 (UTC) '' |
Revision as of 14:20, 16 November 2012
Introduction
On this page you will find a synthetic parametric model for which one can easily experiment with different system orders  , values of the parameter
, values of the parameter  , as well as different poles and residues.
, as well as different poles and residues.
Also, the decay of the Hankel singular values can be changed indirectly through the parameter  .
.
Model description
The parameter  scales the real part of the system poles, that is,
scales the real part of the system poles, that is, 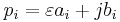 .
For a system in pole-residue form
.
For a system in pole-residue form
we can write down the state-space realization
with system matrices defined as
Notice that the system matrices have complex entries.
For simplicity, assume that  is even,
is even, 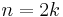 , and that all system poles are complex and ordered in complex conjugate pairs, i.e.
, and that all system poles are complex and ordered in complex conjugate pairs, i.e.
and the residues also form complex conjugate pairs
Then a realization with matrices having real entries is given by
with ![A_{\varepsilon,i} = \left[\begin{array}{cc} a_i& 0 \\ 0 & a_i \end{array}\right]](/morwiki/images/math/c/4/d/c4daf85733e144db5528fb1a97dcc3b1.png) ,
,
![A_{0,i} = \left[\begin{array}{cc} 0& b_i \\ -b_i & 0 \end{array}\right]](/morwiki/images/math/9/c/e/9cefed461140230838eec45e4654af4a.png) ,
,
![B_{i} = \left[\begin{array}{c} 2 \\ 0 \end{array}\right]](/morwiki/images/math/1/6/d/16d6f95252fffc0c7217cb71546f9dff.png) ,
,
![C_{i} = \left[\begin{array}{cc} c_i& d_i\end{array}\right]](/morwiki/images/math/3/b/7/3b78f9392f071a38a8ecf9d7d1af9ee6.png) .
.
Numerical values
We construct a system of order 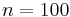 . The numerical values for the different variables are
. The numerical values for the different variables are
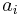 equally spaced in
equally spaced in ![[-10^3, -10]](/morwiki/images/math/0/1/e/01eb0216a83386dce806710ccd49014d.png) ,
,
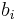 equally spaced in
equally spaced in ![[10, 10^3]](/morwiki/images/math/0/b/e/0be1e9dea133f5e55f228e67a2ea56b4.png) ,
,
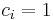 ,
,
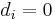 ,
,

![\in [1/50,1]](/morwiki/images/math/3/4/0/3409a13a32f034288c27700bb927d09e.png) .
.
In MATLAB, the system matrices are easily formed as follows:
n = 100;
a = -linspace(1e1,1e3,n/2).'; b = linspace(1e1,1e3,n/2).';
c = ones(n/2,1); d = zeros(n/2,1);
aa(1:2:n-1,1) = a; aa(2:2:n,1) = a;
bb(1:2:n-1,1) = b; bb(2:2:n-2,1) = 0;
Ae = spdiags(aa,0,n,n);
A0 = spdiags([0;bb],1,n,n) + spdiags(-bb,-1,n,n);
B = 2*sparse(mod([1:n],2)).';
C(1:2:n-1) = c.'; C(2:2:n) = d.'; C = sparse(C);
The above system matrices 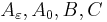 are also available in MatrixMarket format Synth_matrices.tar.gz.
are also available in MatrixMarket format Synth_matrices.tar.gz.
Plots
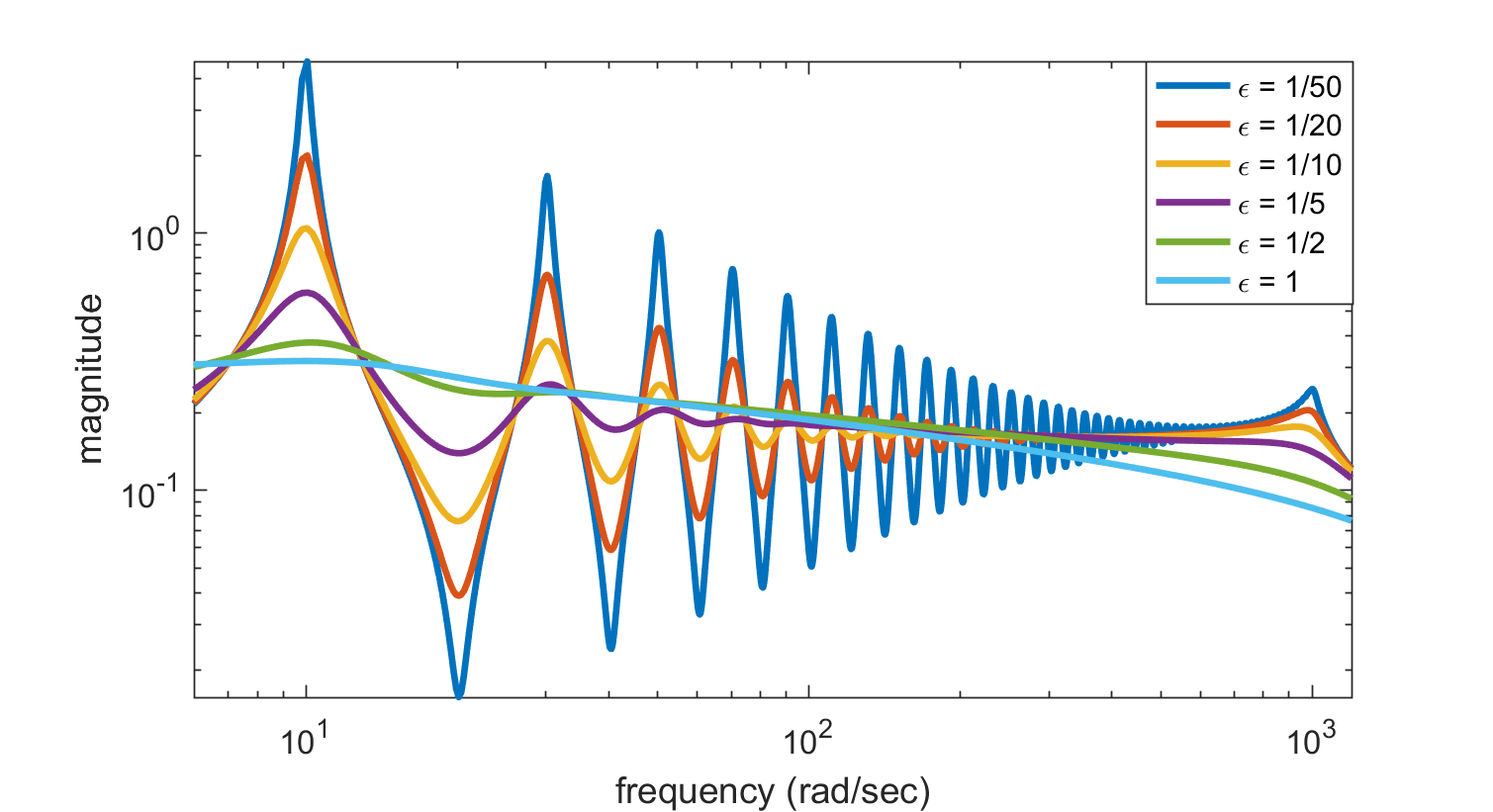
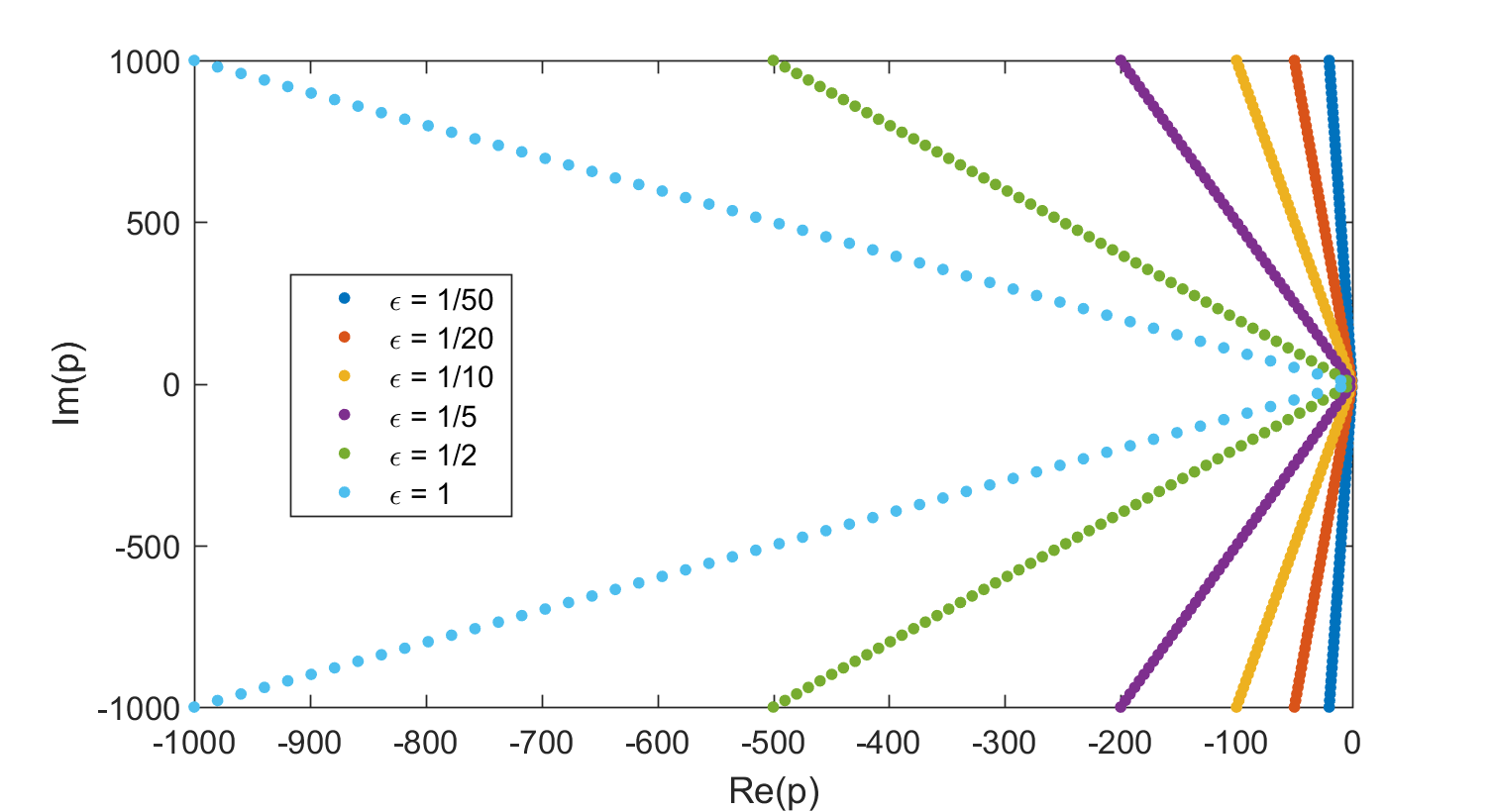
We plot the frequency response 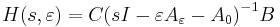 and poles for parameter values
and poles for parameter values ![\varepsilon \in [1/50, 1/20, 1/10, 1/5, 1/2, 1]](/morwiki/images/math/1/f/7/1f7392c05a89973f3622df1b8cd09a32.png) .
.
In MATLAB, the plots are generated using the following commands:
r(1:2:n-1,1) = c+1j*d; r(2:2:n,1) = c-1j*d;
ep = [1/50; 1/20; 1/10; 1/5; 1/2; 1]; % parameter epsilon
jw = 1j*linspace(0,1.2e3,5000).'; % frequency grid
for j = 1:length(ep)
p(:,j) = [ep(j)*a+1j*b; ep(j)*a-1j*b]; % poles
[jww,pp] = meshgrid(jw,p(:,j));
Hjw(j,:) = (r.')*(1./(jww-pp)); % freq. resp.
end
figure, loglog(imag(jw),abs(Hjw),'LineWidth',2)
axis tight, xlim([6 1200])
xlabel('frequency (rad/sec)')
ylabel('magnitude')
title('Frequency response for different \epsilon')
figure, plot(real(p),imag(p),'.')
title('Poles for different \epsilon')
Other interesting plots result for small values of the parameter. For example, for 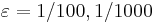 , the peaks in the frequency response become more pronounced, since the poles move closer to the imaginary axis.
, the peaks in the frequency response become more pronounced, since the poles move closer to the imaginary axis.
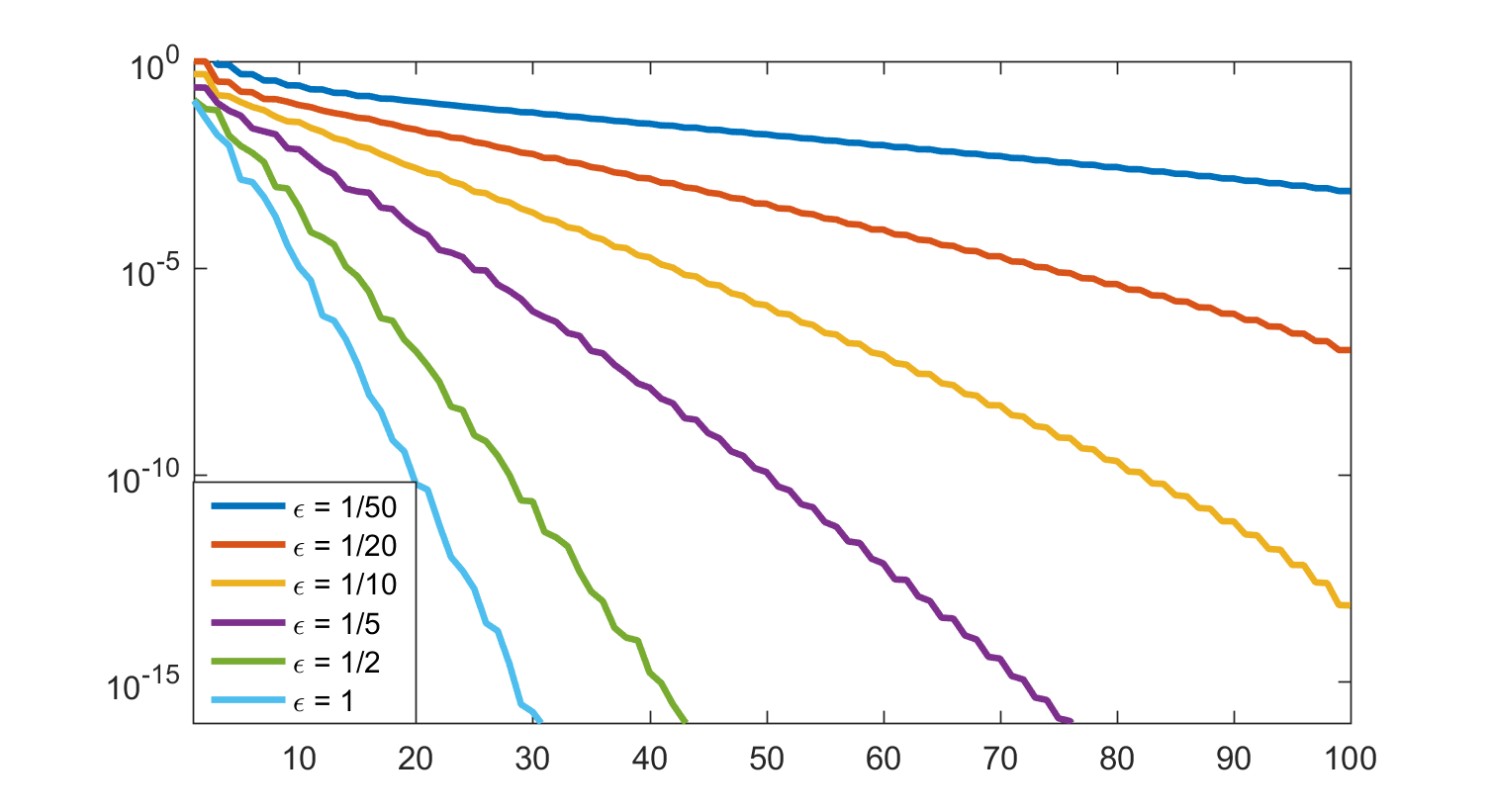
Next, for ![\varepsilon \in [1/50, 1/20, 1/10, 1/5, 1/2, 1]](/morwiki/images/math/1/f/7/1f7392c05a89973f3622df1b8cd09a32.png) , we also plot the decay of the Hankel singular values. Notice that for small values of the parameter, the decay of the Hankel singular values is very slow.
, we also plot the decay of the Hankel singular values. Notice that for small values of the parameter, the decay of the Hankel singular values is very slow.
Contact information:
Antonio Cosmin Ionita 14:38, 29 November 2011 (UTC)

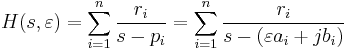
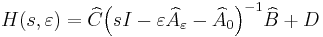
![\varepsilon \widehat{A}_\varepsilon + \widehat{A}_0 = \varepsilon \left[\begin{array}{ccc} a_1 & & \\ & \ddots & \\ & & a_n\end{array}\right] +\left[\begin{array}{ccc} jb_1 & & \\ & \ddots & \\ & & jb_n\end{array}\right] ,](/morwiki/images/math/7/9/0/790c70f3fdd1a7fe269be673f52f5e8c.png)
![\widehat{B} = [1,\ldots,1]^T,\quad \widehat{C} = [r_1,\ldots,r_n],\quad D = 0.](/morwiki/images/math/0/1/9/01952f4b905489c1f4686227dc13e409.png)
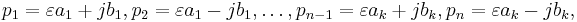
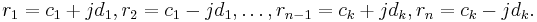
![A_\varepsilon = \left[\begin{array}{ccc} A_{\varepsilon,1} & & \\ & \ddots & \\ & & A_{\varepsilon,k}\end{array}\right], \quad A_0 = \left[\begin{array}{ccc} A_{0,1} & & \\ & \ddots & \\ & & A_{0,k}\end{array}\right], \quad B = \left[\begin{array}{c} B_1 \\ \vdots \\ B_k\end{array}\right], \quad C = \left[\begin{array}{ccc} C_1 & \cdots & C_k\end{array}\right], \quad D = 0,](/morwiki/images/math/f/2/4/f24f26251cc0c24bed73a958735c4681.png)