m (infobox string) |
m (infobox string edit) |
||
| Line 6: | Line 6: | ||
{{Infobox |
{{Infobox |
||
| − | |Title = |
+ | |Title = Sound Transmission through a Plate |
| − | |Benchmark ID = |
+ | |Benchmark ID = soundTransmission_n95480m1q1 |
|Category = misc |
|Category = misc |
||
| − | |System-Class = |
+ | |System-Class = LTI-SOS |
| − | |nstates = |
+ | |nstates = 95480 |
|ninputs = 1 |
|ninputs = 1 |
||
| − | |noutputs = |
+ | |noutputs = 1 |
| − | |nparameters = |
+ | |nparameters = 0 |
| − | |components = |
+ | |components = B, C, E, K, M |
| − | |License = |
+ | |License = Creative Commons Attribution 4.0 International |
| − | |Creator = [[User: |
+ | |Creator = [[User:Aumann]] |
|Editor = |
|Editor = |
||
| − | * [[User: |
+ | * [[User:Aumann]] |
| + | |Zenodo-link = https://zenodo.org/record/7670587/files/soundTransmission_n95480m1q1.mat |
||
| − | * [[User:Himpe]] |
||
| − | |Zenodo-link = NA |
||
}} |
}} |
||
Latest revision as of 10:41, 30 November 2023
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
| Background | |
|---|---|
| Benchmark ID |
soundTransmission_n95480m1q1 |
| Category |
misc |
| System-Class |
LTI-SOS |
| Parameters | |
| nstates |
95480
|
| ninputs |
1 |
| noutputs |
1 |
| nparameters |
0 |
| components |
B, C, E, K, M |
| Copyright | |
| License |
Creative Commons Attribution 4.0 International |
| Creator | |
| Editor | |
| Location | |
|
https://zenodo.org/record/7670587/files/soundTransmission_n95480m1q1.mat | |
Description
The Sound transmission through a plate benchmark models the radiation of a vibrating plate and the excitation of a structure by an oscillating acoustic fluid. It is based on an experiment by Guy[1].
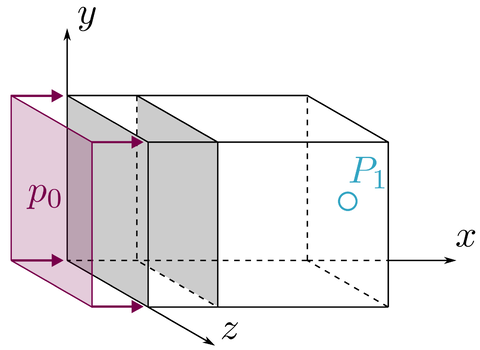
The system consists of a cuboid acoustic cavity, where one wall is considered a system of two parallel elastic brass plates with a 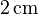 air gap between them; all other walls are considered rigid. The plates measure
air gap between them; all other walls are considered rigid. The plates measure 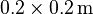 and have a thickness of
and have a thickness of 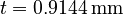 ; the receiving cavity is
; the receiving cavity is  wide. The outer plate is excited by a uniform pressure load and the resulting acoustic pressure in the receiving cavity is measured at the middle of the rigid wall opposite to the elastic plate (
wide. The outer plate is excited by a uniform pressure load and the resulting acoustic pressure in the receiving cavity is measured at the middle of the rigid wall opposite to the elastic plate ( in the sketch).
in the sketch).
The following material parameters have been considered for the brass plates and the acoustic fluid:
| Part | Parameter | Value | Unit |
| Brass plates | 
|

|

|

|

|
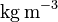
| |

|
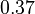
|

| |
| Acoustic fluid | 
|

|
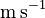
|

|

|
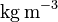
|
Dimensions
System structure:
System dimensions:
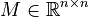 ,
,
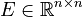 ,
,
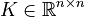 ,
,
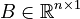 ,
,
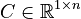 ,
with
,
with 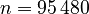 .
.
Proportional damping, i.e. 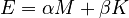 , with
, with 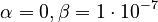 is considered.
The two-way coupling between the structure and the acoustic fluid results in non-symmetric matrices
is considered.
The two-way coupling between the structure and the acoustic fluid results in non-symmetric matrices  .
.
Data
The data is available at Zenodo.
Remarks
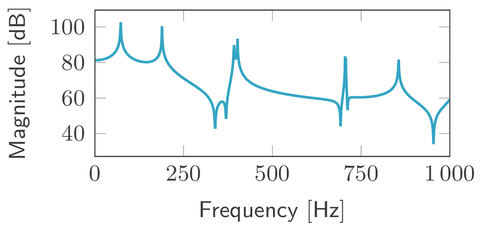
- The numerical model resembles the experimental data[1] in a frequency range from
 to
to  . The frequency response in this range is also included in the dataset.
. The frequency response in this range is also included in the dataset. - The finite element discretization has been performed with Kratos Multiphysics.
- The system has unstable eigenvalues. This is common in interior acoustic problems where no damping is assumed for the acoustic fluid[2].
- A comparison of different interpolation-based MOR methods using this benchmark example is available in[3]
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
@Misc{dataAum22,
author = {Aumann, Q.},
title = {Matrices for a sound transmission problem},
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
year = 2022,
doi = {10.5281/zenodo.7300346}
}
- For the background on the benchmark:
@Article{AumW23,
author = {Aumann, Q. and Werner, S.~W.~R.},
title = {Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods},
journal = {Journal of Sound and Vibration},
volume = 543,
year = 2023,
pages = {117363},
doi = {10.1016/j.jsv.2022.117363},
publisher = {Elsevier {BV}}
}
References
- ↑ 1.0 1.1 R. W. Guy. "The Transmission of Airborne Sound through a Finite Panel, Air Gap, Panel and Cavity Configuration – a Steady State Analysis ", Acta Acustica united with Acustica, 49(4): 323--333, 1981.
- ↑ V. Cool, S. Jonckheere, E. Deckers, W. Desmet. "Black box stability preserving reduction techniques in the Loewner framework for the efficient time domain simulation of dynamical systems with damping treatments", Journal of Sound and Vibration, 529: 116922, 2022.
- ↑ Q. Aumann, S. W. R. Werner. "Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods", Journal of Sound and Vibration, 543: 117363, 2023.