| Line 12: | Line 12: | ||
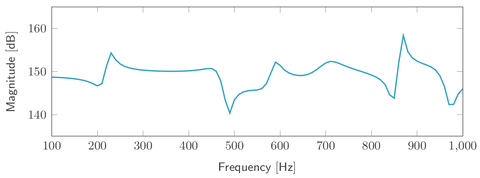
The '''Porous absorber''' benchmark models the sound pressure in a cavity excited by a single harmonic load. One side of the cavity is covered by a layer of poroelastic material, which adds dissipation to the system. The geometry of this model follows <ref name="rumpler14"/>. Various projection-based model order reduction methods have been applied and compared using this example as a benchmark in <ref name="aumann23"/>. |
The '''Porous absorber''' benchmark models the sound pressure in a cavity excited by a single harmonic load. One side of the cavity is covered by a layer of poroelastic material, which adds dissipation to the system. The geometry of this model follows <ref name="rumpler14"/>. Various projection-based model order reduction methods have been applied and compared using this example as a benchmark in <ref name="aumann23"/>. |
||
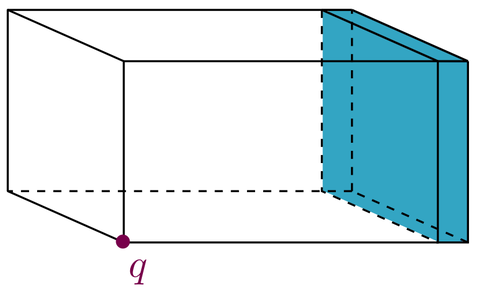
| + | The cavity has the dimensions <math>0.75 \times 0.6 \times 0.4\,\mathrm{m}</math> and one wall is covered by a <math>0.05\,\mathrm{m}</math> thick poroelastic layer acting as a sound absorber. The poroelastic material is described by the Biot theory<ref name="biot56"/> and the system is excited by a point source located in a corner opposite of the porous layer. |
||
==References== |
==References== |
||
| Line 20: | Line 21: | ||
<ref name="aumann23">Q. Aumann, S. W. R. Werner. "<span class="plainlinks">[https://doi.org/10.1016/j.jsv.2022.117363 Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods]</span>", Journal of Sound and Vibration, 543: 117363, 2023.</ref> |
<ref name="aumann23">Q. Aumann, S. W. R. Werner. "<span class="plainlinks">[https://doi.org/10.1016/j.jsv.2022.117363 Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods]</span>", Journal of Sound and Vibration, 543: 117363, 2023.</ref> |
||
| + | |||
| + | <ref name="biot56">M. A. Biot. "<span class="plainlinks">[http://dx.doi.org/10.1121/1.1908239 Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range]</span>", J. Acoust. Soc. Am., 28(2):168–178, 1956.</ref> |
||
</references> |
</references> |
||
Revision as of 16:09, 27 June 2023
Note: This page has not been verified by our editors.
.
Description
The Porous absorber benchmark models the sound pressure in a cavity excited by a single harmonic load. One side of the cavity is covered by a layer of poroelastic material, which adds dissipation to the system. The geometry of this model follows [1]. Various projection-based model order reduction methods have been applied and compared using this example as a benchmark in [2].
The cavity has the dimensions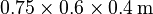 
and one wall is covered by a 
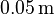thick poroelastic layer acting as a sound absorber. The poroelastic material is described by the Biot theory[3] and the system is excited by a point source located in a corner opposite of the porous layer.
References
- ↑ R. Rumpler, P. Göransson, J.-F. Deü. "A finite element approach combining a reduced-order system, Padé approximants, and an adaptive frequency windowing for fast multi-frequency solution of poro-acoustic problems", International Journal for Numerical Methods in Engineering, 97: 759-784, 2014.
- ↑ Q. Aumann, S. W. R. Werner. "Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods", Journal of Sound and Vibration, 543: 117363, 2023.
- ↑ M. A. Biot. "Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range", J. Acoust. Soc. Am., 28(2):168–178, 1956.