(Update dataset doi) |
|||
| Line 64: | Line 64: | ||
==Data== |
==Data== |
||
| − | The data is available at [https://doi.org/10.5281/zenodo. |
+ | The data is available at [https://doi.org/10.5281/zenodo.7507011 Zenodo]. |
==Remarks== |
==Remarks== |
||
| Line 81: | Line 81: | ||
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki}, |
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki}, |
||
year = 2023, |
year = 2023, |
||
| − | doi = {10.5281/zenodo. |
+ | doi = {10.5281/zenodo.7507011} |
} |
} |
||
Revision as of 19:39, 23 February 2023
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description
The Plate with tuned vibration absorbers benchmark models the vibration response of a plate excited by a single harmonic load. The plate is equipped with 108 tuned vibration absorbers (TVA), which change the vibration pattern of the host structure in a narrow frequency band around their tuning frequency[1]. Such systems have, for example, been examined in [2] and [3].
This benchmark models an aluminum plate with dimensions  and a thickness of
and a thickness of 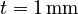 . The surrounding edges are simply supported. The plate's surface is equipped with six struts along the
. The surrounding edges are simply supported. The plate's surface is equipped with six struts along the 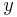 -direction, on which the TVAs are placed. The TVAs have a combined mass of
-direction, on which the TVAs are placed. The TVAs have a combined mass of 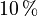 of the plate mass and are tuned to
of the plate mass and are tuned to 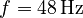 . The plate is excited by a single load near one of the corners of the plate (see sketch). The root mean square of the displacement in
. The plate is excited by a single load near one of the corners of the plate (see sketch). The root mean square of the displacement in 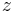 -direction at all points of the plate surface is plotted in Figure 2. The effect of the TVAs is clearly visible in the frequency range around their tuning frequency.
-direction at all points of the plate surface is plotted in Figure 2. The effect of the TVAs is clearly visible in the frequency range around their tuning frequency.
The following material parameters have been considered for aluminum:
| Parameter | Value | Unit |

|

|

|

|
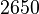
|
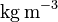
|

|

|

|
Dimensions
System structure:
System dimensions:
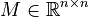 ,
,
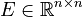 ,
,
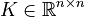 ,
,
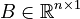 ,
,
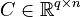 ,
with
,
with 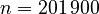 and
and 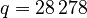 .
.
Proportional damping, i.e. 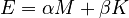 , with
, with 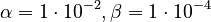 is considered.
The matrices
is considered.
The matrices  are positive (semi-) definite.
are positive (semi-) definite.
Data
The data is available at Zenodo.
Remarks
- The dataset also contains a version with a single output (SISO). Here, the displacement of the plate at the location of the load is evaluated.
- The frequency response in the range
 to
to 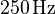 is included in the dataset.
is included in the dataset. - The finite element discretization has been performed with Kratos Multiphysics.
- A comparison of different interpolation-based MOR methods using this benchmark example is available in [4]
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
@Misc{dataAum23,
author = {Aumann, Q.},
title = {Matrices for a plate with tuned vibration absorbers},
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
year = 2023,
doi = {10.5281/zenodo.7507011}
}
- For the background on the benchmark:
@Article{AumW23,
author = {Aumann, Q. and Werner, S.~W.~R.},
title = {Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods},
journal = {Journal of Sound and Vibration},
volume = 543,
year = 2023,
pages = {117363},
doi = {10.1016/j.jsv.2022.117363},
publisher = {Elsevier {BV}}
}
References
- ↑ J. Q. Sun, M. R. Jolly, M. A. Norris. "Passive, Adaptive and Active Tuned Vibration Absorbers—A Survey", Journal of Mechanical Design, 117.B: 234–242, 1995.
- ↑ D. J. Jagodzinski, M. Miksch, Q. Aumann, G. Müller. "Modeling and optimizing an acoustic metamaterial to minimize low-frequency structure-borne sound", Mechanics Based Design of Structures and Machines, 50(8): 2877–2891, 2020.
- ↑ C. Claeys, E. Deckers, B. Pluymers, W. Desmet. "A lightweight vibro-acoustic metamaterial demonstrator: Numerical and experimental investigation", Mechanical Systems and Signal Processing, 70-71: 853–880, 2016.
- ↑ Q. Aumann, S. W. R. Werner. "Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods", Journal of Sound and Vibration, 543: 117363, 2023.



