(→Description: change f to B) |
(replace K_d with K, and -M with M (to be consistent with SOS model); replace B^T with C) |
||
| Line 15: | Line 15: | ||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | + | K x + \omega^2 M x & = B \\ |
|
| − | y & = |
+ | y & = C x |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| − | where <math>B</math> represents a unit point load in one unknown of the state vector |
+ | where <math>B</math> represents a unit point load in one unknown of the state vector, <math>C = B^T </math>, |
| − | <math>M</math> is a symmetric positive-definite matrix and <math> |
+ | <math>M</math> is a symmetric positive-definite matrix, and <math>K = (1+i\gamma) \widetilde{K}</math> with <math>\widetilde{K}</math> symmetric positive semidefinite. |
The test problem is a structural model of a car windscreen. <ref name="meerbergen2007"/> |
The test problem is a structural model of a car windscreen. <ref name="meerbergen2007"/> |
||
| Line 50: | Line 50: | ||
* [https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Windscreen-dim1e4-windscreen.tar.gz Windscreen-dim1e4-windscreen.tar.gz] (21.5 MB) |
* [https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Windscreen-dim1e4-windscreen.tar.gz Windscreen-dim1e4-windscreen.tar.gz] (21.5 MB) |
||
| − | The archive contains files <tt>windscreen.K</tt>, <tt>windscreen.M</tt> and <tt>windscreen.B</tt> representing <math> |
+ | The archive contains files <tt>windscreen.K</tt>, <tt>windscreen.M</tt> and <tt>windscreen.B</tt> representing <math>K</math>, <math>M</math> and <math>B</math> accordingly. |
==Dimensions== |
==Dimensions== |
||
| Line 58: | Line 58: | ||
\begin{align} |
\begin{align} |
||
(K + \omega^2 M) x & = B \\ |
(K + \omega^2 M) x & = B \\ |
||
| − | y & = |
+ | y & = C x |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| Line 67: | Line 67: | ||
<math>K \in \mathbb{C}^{22692 \times 22692}</math>, |
<math>K \in \mathbb{C}^{22692 \times 22692}</math>, |
||
<math>M \in \mathbb{R}^{22692 \times 22692}</math>, |
<math>M \in \mathbb{R}^{22692 \times 22692}</math>, |
||
| − | <math>B \in \mathbb{R}^{22692 \times 1}</math> |
+ | <math>B \in \mathbb{R}^{22692 \times 1}</math>, |
| + | <math>C \in \mathbb{R}^{1 \times 22692}</math>, |
||
==Citation== |
==Citation== |
||
Revision as of 15:34, 31 August 2022
Description
This is an example for a model in the frequency domain of the form
\[ \begin{align} K x + \omega^2 M x & = B \\ y & = C x \end{align} \]
where \(B\) represents a unit point load in one unknown of the state vector, \(C = B^T \), \(M\) is a symmetric positive-definite matrix, and \(K = (1+i\gamma) \widetilde{K}\) with \(\widetilde{K}\) symmetric positive semidefinite.
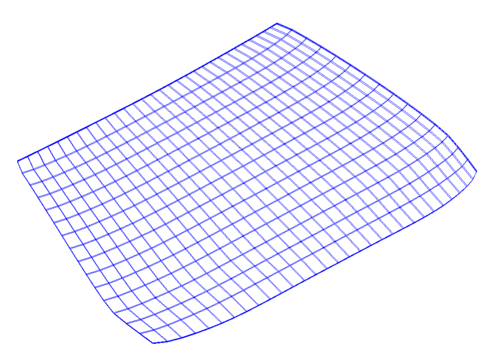
The test problem is a structural model of a car windscreen. [1] This is a 3D problem discretized with \(7564\) nodes and \(5400\) linear hexahedral elements (3 layers of \(60 \times 30\) elements). The mesh is shown in Fig. 1. The material is glass with the following properties: The Young modulus is \(7\times10^{10}\mathrm{N}/\mathrm{m}^2\), the density is \(2490 \mathrm{kg}/\mathrm{m}^3\), and the Poisson ratio is \(0.23\). The natural damping is \(10\%\), i.e. \(\gamma=0.1\). The structural boundaries are free (free-free boundary conditions). The windscreen is subjected to a point force applied on a corner. The goal of the model reduction is the fast evaluation of \(y\). Model reduction is used as a fast linear solver for a sequence of parametrized linear systems.
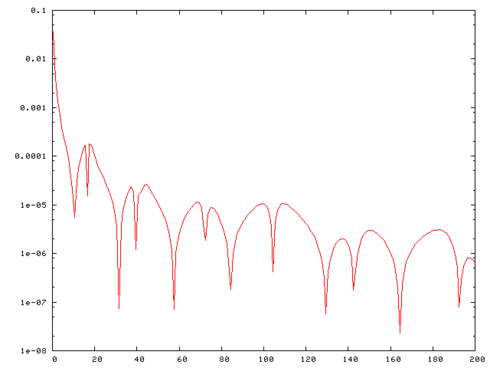
The discretized problem has dimension \(n=22692\). The goal is to estimate \(x(\omega)\) for \(\omega\in[0.5,200]\). In order to generate the plots, the frequency range was discretized as \(\{\omega_1,\ldots,\omega_m\} = \{0.5j,j=1,\ldots,m\}\) with \(m=400\).
Fig. 1 shows the mesh of the car windscreen and Fig. 2 the frequency response \(\vert \Re(y(\omega)) \vert\).
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[2]; No. 38886.
Data
Download matrices in the Matrix Market format:
- Windscreen-dim1e4-windscreen.tar.gz (21.5 MB)
The archive contains files windscreen.K, windscreen.M and windscreen.B representing \(K\), \(M\) and \(B\) accordingly.
Dimensions
System structure: \[ \begin{align} (K + \omega^2 M) x & = B \\ y & = C x \end{align} \] with \(\omega \in [0.5, 200]\).
System dimensions\[K \in \mathbb{C}^{22692 \times 22692}\], \(M \in \mathbb{R}^{22692 \times 22692}\), \(B \in \mathbb{R}^{22692 \times 1}\), \(C \in \mathbb{R}^{1 \times 22692}\),
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Oberwolfach Benchmark Collection, Windscreen. hosted at MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Windscreen
@MISC{morwiki_windscreen,
author = {{Oberwolfach Benchmark Collection}},
title = {Windscreen},
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/Windscreen},
year = 20XX
}
- For the background on the benchmark:
@article{Mee07,
author = {K. Meerbergen},
title = {Fast frequency response computation for {R}ayleigh damping},
journal = {International Journal for Numerical Methods in Engineering},
volume = {73},
number = {1},
pages = {96--106},
year = {2007},
doi = {10.1002/nme.2058},
}
References
- ↑ K. Meerbergen, Fast frequency response computation for Rayleigh damping, International Journal for Numerical Methods in Engineering, 73(1): 96--106, 2007.
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, In: Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.