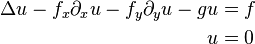Convection-Diffusion

Description

The Convection-Diffusion benchmark is given by a finite-difference discretization of a two-dimensional dynamic convection-diffusion heat equation on a unit square domain, which was introduced as a example in :

$\begin{align} \Delta u - f_x \partial_x u - f_y \partial_y u - g u &= f \\ u &= 0 \end{align}$

For this procedural partial differential equation benchmark Dirichlet boundary conditions are used. The setup of this benchmark is rather generic, in that it allows based on the configuration of 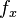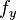$f_x$, $f_y$, $g$ and $f$ to tune the influence of the diffusive, convective and reactive differential operators.

Origin

This benchmark is part of LYAPACK .

Data

In the folder examples of LYAPCK the MATLAB functions fdm_2d_matrix and fdm_2d_vector are utilized to generate the system, input matrices:

A = fdm_2d_matrix(n0,fx_str,fy_str,g_str);
B = fdm_2d_vector(n0,f_str);

The no argument determines the common spatial resolution, hence the discretized problem has dimension 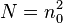$N = n_0^2$. The arguments fx_str, fy_str, g_str, and f_str are strings (see documentation) describing the convection in the first dimension, second dimension, the reaction coefficient and the source term respectively. The output matrix can be generated in the same fashaion as the input matrix.

For example, in , the examples are constructed with:

A = fdm_2d_matrix(20,'10*x','100*y','0');
B = fdm_2d_vector(20,'.1<x<=.3'); 
C = fdm_2d_vector(20,'.7<x<=.9')'; 

resulting in a SISO system of order 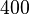$400$.

Dimensions

System structure:

$\begin{align} \dot{x}(t) &= Ax(t) + Bu(t) \\ y(t) &= Cx(t) \end{align}$

System dimensions:

$A \in \mathbb{R}^{N \times N}$, $B \in \mathbb{R}^{N \times 1}$, $C \in \mathbb{R}^{1 \times N}$.

Citation

To cite this benchmark, use the following references:

• For the benchmark:

The MORwiki Community, LYAPACK - A MATLAB Toolbox for Large Lyapunov and Riccati Equations, Model Reduction Problems, and Linear–Quadratic Optimal Control Problems. Version 1.0, netlib, 1999. http://www.netlib.org/lyapack

@MISC{lyapack,
  author =       {T. Penzl},
  title =        {LYAPACK - A MATLAB Toolbox for Large Lyapunov and Riccati Equations, Model Reduction Problems, and Linear–Quadratic Optimal Control Problems},
  howpublished = {netlib},
  note =         {Version 1.0},
  url =          {http://www.netlib.org/lyapack},
  year =         {1999}
}