| Line 36: | Line 36: | ||
The matrix $V$ is derived by orthogonalizing a number of moment |
The matrix $V$ is derived by orthogonalizing a number of moment |
||
| − | matrices of the system in |
+ | matrices of the system in (1)[1][2]. |
| − | (\ref{linear1})\cite{FengB07, Daniel04}. |
||
| − | By defining |
+ | By defining <math>B_M=\tilde{E}^{-1}B, M_i=-\tilde{E}^{-1}E_i,i=1,2,\ldots,p</math> and |
| + | |||
| − | $i=1,2,\ldots,p$ and |
||
| + | <math> |
||
| − | % |
||
| + | \tilde{E}=E_0+s_1^0E_1+s_2^0E_2+\cdots+s_p^0E_p, |
||
| − | % |
||
| + | </math> |
||
| − | \begin{equation} |
||
| + | |||
| − | \label{E} |
||
| + | we can expand <math>x</math> in (1) at <math>s_1, s_2, \ldots, s_p</math> around a set of |
||
| − | \tilde{E}=E_0+s_1^0E_1+s_2^0E_2+\cdots+s_p^0E_p |
||
| + | expansion points <math>p_0=[s_1^0,s_2^0,\cdots,s_p^0]</math> as below, |
||
| − | \end{equation} |
||
| + | |||
| − | % |
||
| + | <math> |
||
| − | % |
||
| + | x=[I-(\sigma_1M_1+\ldots +\sigma_pM_p]^{-1}B_Mu(s_p) |
||
| − | we can expand $x$ in (\ref{linear1}) at $s_1, s_2, \ldots, s_p$ around a set of |
||
| + | =\sum\limits_{i=0}^{\infty}(\sigma_1M_1+\ldots+\sigma_pM_p)^iB_Mu(s_p). |
||
| − | expansion points $p_0=[s_1^0,s_2^0,\cdots,s_p^0]$ as below, |
||
| + | </math> |
||
| − | % |
||
| + | |||
| − | % |
||
| + | Here <math>\sigma_i=s_i-s_i^0, i=1,2,\ldots,p</math>. We call the coefficients |
||
| − | \begin{equation} |
||
| + | in the above series expansion moment matrices of the parametrized |
||
| − | \label{x1} |
||
| + | system, i.e. <math>B_M, \ M_1B_M, \ \ldots, \ M_pB_M,\ M_1^2B_M, \ |
||
| − | \begin{array}{rl} |
||
| − | x&=[I-(\sigma_1M_1+\ldots +\sigma_pM_p]^{-1}B_Mu(s_p)\\ |
||
| − | &=\sum\limits_{i=0}^{\infty}(\sigma_1M_1+\ldots+\sigma_pM_p)^iB_Mu(s_p).\\ |
||
| − | \end{array} |
||
| − | \end{equation} |
||
| − | % |
||
| − | % |
||
| − | Here $\sigma_i=s_i-s_i^0, i=1,2,\ldots,p$. We call the coefficients |
||
| − | in the above series expansion moment matrices of the parameterized |
||
| − | system, i.e. $B_M, \ M_1B_M, \ \ldots, \ M_pB_M,\ M_1^2B_M, \ |
||
(M_1M_2+M_2M_1)B_M, \ \ldots, \ (M_1M_p+M_pM_1)B_M, \ M_p^2B_M, \ |
(M_1M_2+M_2M_1)B_M, \ \ldots, \ (M_1M_p+M_pM_1)B_M, \ M_p^2B_M, \ |
||
| − | M_1^3B_M, \ \ldots |
+ | M_1^3B_M, \ \ldots</math>. The corresponding moments are those moment |
| − | matrices multiplied by |
+ | matrices multiplied by <math>L^{\mathrm{T}}</math> from the left. The matrix <math>V</math> can be |
generated by first explicitly computing some of the moment matrices |
generated by first explicitly computing some of the moment matrices |
||
and then orthogonalizing them as is suggested in~\cite{Daniel04}. |
and then orthogonalizing them as is suggested in~\cite{Daniel04}. |
||
The resulting $V$ is desired to expand the subspace: |
The resulting $V$ is desired to expand the subspace: |
||
| + | |||
| − | % |
||
| + | <math> |
||
| − | % |
||
| + | \mathop{\mathrm{range}}\{V\}=\mathop{\mathrm{span}}\{B_M, \ M_1B_M,\ldots, M_pB_M,\ M_1^2B_M, |
||
| − | \begin{equation} |
||
| + | (M_1M_2+M_2M_1)B_M, \ldots, (M_1M_p+M_pM_1)B_M, |
||
| − | \label{v1} |
||
| + | M_p^2B_M, M_1^3B_M,\ldots, M_1^rB_M, \ldots,M_p^rB_M \}. (2) |
||
| − | \begin{array}{rl} |
||
| + | </math> |
||
| − | \mathop{\mathrm{range}}\{V\}=&\mathop{\mathrm{span}}\{B_M, \ M_1B_M,\ldots, M_pB_M,\ M_1^2B_M, \\ |
||
| + | |||
| − | & (M_1M_2+M_2M_1)B_M, \ldots, (M_1M_p+M_pM_1)B_M, \\ |
||
| + | However, <math>V</math> does not really span the whole subspace, because the |
||
| − | & M_p^2B_M, M_1^3B_M,\ldots, M_1^rB_M, \ldots,M_p^rB_M \}. |
||
| − | \end{array} |
||
| − | \end{equation} |
||
| − | % |
||
| − | % |
||
| − | However, $V$ does not really span the whole subspace, because the |
||
latterly computed vectors in the subspace become linearly dependent |
latterly computed vectors in the subspace become linearly dependent |
||
| − | due to numerical instability. Therefore, with this matrix |
+ | due to numerical instability. Therefore, with this matrix <math>V</math> one |
cannot get an accurate reduced model which matches all the moments |
cannot get an accurate reduced model which matches all the moments |
||
included in the subspace. |
included in the subspace. |
||
| − | Instead of directly computing the moment matrices in ( |
+ | Instead of directly computing the moment matrices in (2)[1], a |
| − | numerically robust method is proposed in |
+ | numerically robust method is proposed in [1] (the |
| − | detailed algorithm is described in |
+ | detailed algorithm is described in [3]), which combines |
| − | the recursions in ( |
+ | the recursions in (4) with the modified Gram-Schmidt |
| − | process to implicitly compute the moment matrices. The computed |
+ | process to implicitly compute the moment matrices. The computed <math>V</math> |
is actually an orthonormal basis of the subspace as below, |
is actually an orthonormal basis of the subspace as below, |
||
| + | |||
| − | % |
||
| + | <math> |
||
| − | % |
||
| + | \mathop{\mathrm{range}}\{V\}=\mathop{\mathrm{span}}\{R_0, R_1,\ldots, R_r \}. (3) |
||
| − | \begin{equation} |
||
| + | </math> |
||
| − | \label{v2} |
||
| + | |||
| − | \mathop{\mathrm{range}}\{V\}=\mathop{\mathrm{span}}\{R_0, R_1,\ldots, R_r \}. |
||
| + | It can be proved that the subspace in~(2) is included in the |
||
| − | \end{equation} |
||
| + | subspace in~(3). Due to the numerical stability properties of |
||
| − | % |
||
| − | % |
||
| − | It can be proved that the subspace in~(\ref{v1}) is included in the |
||
| − | subspace in~(\ref{v2}). Due to the numerical stability properties of |
||
the repeated modified Gram-Schmidt process employed in |
the repeated modified Gram-Schmidt process employed in |
||
| − | + | [2][3], the reduced model derived from <math>V</math> |
|
| − | in~( |
+ | in~(3) is computed in a numerically stable and accurate way. |
| + | |||
| − | % |
||
| + | <math> |
||
| − | % |
||
| + | R_0=B_M, \ R_1=[M_1R_0,\ldots, M_pR_0], |
||
| − | \begin{equation} |
||
| + | R_2=[M_1R_1,\ldots, M_pR_1], |
||
| − | \label{moments} |
||
| + | \vdots, |
||
| − | \begin{array}{l} |
||
| − | + | R_r=[M_1R_{r-1},\ldots, M_pR_{r-1}] |
|
| − | R_2=[M_1R_1,\ldots, M_pR_1], \\ |
||
| − | \vdots, \\ |
||
| − | R_r=[M_1R_{r-1},\ldots, M_pR_{r-1}]\\ |
||
\vdots. |
\vdots. |
||
| + | </math> |
||
| − | \end{array} |
||
| + | |||
| − | \end{equation} |
||
| − | % |
||
| − | % |
||
Furthermore, one can see that each moment matrix is actually several |
Furthermore, one can see that each moment matrix is actually several |
||
| − | vectors multiplied by |
+ | vectors multiplied by <math>\tilde{E}^{-1}</math>, and if the dimension of |
| − | + | <math>\tilde{E}</math> is very large, it is necessary to solve linear systems |
|
like |
like |
||
| + | |||
| − | % |
||
| + | <math> |
||
| − | % |
||
| − | \begin{equation} |
||
\label{sequence} \tilde{E}x=w_i, \ i=1,2,\ldots, l |
\label{sequence} \tilde{E}x=w_i, \ i=1,2,\ldots, l |
||
| + | </math> |
||
| − | \end{equation} |
||
| + | |||
| − | % |
||
| + | to obtain <math>\tilde{E}^{-1}w_i</math>, where <math>\tilde{E}</math> is generally |
||
| − | % |
||
| + | non-symmetric and <math>w_i</math> is a vector. Moreover, if quite a few of the |
||
| − | to obtain $\tilde{E}^{-1}w_i$, where $\tilde{E}$ is generally |
||
| − | nonsymmetric and $w_i$ is a vector. Moreover, if quite a few of the |
||
moment matrices need to be computed (this is normal when system |
moment matrices need to be computed (this is normal when system |
||
| − | ( |
+ | (1) contains more than 2 parameters), the number <math>l</math> of |
| − | the linear systems in (\ref{sequence}) will be very large. |
+ | the linear systems in (\ref{sequence}) will be very large. |
| − | looking at the above recursions in~(\ref{moments}), it is obvious that the right-hand |
||
| − | sides of the linear systems cannot be available simultaneously. |
||
| − | Systems in (\ref{sequence}) can be simply solved one after another |
||
| − | by standard iterative methods such as GMRES. However, it is possible |
||
| − | to speed up the standard iterative methods by using more efficient |
||
| − | methods. |
||
Revision as of 16:49, 29 November 2011
Parametric model order reduction (PMOR) methods are designed for model order reduction of parametrized systems, where the parameters of the system play an important role in practical applications such as Integrated Circuit (IC) design, MEMS design, Chemical engineering etc.. The parameters could be the variables describing geometrical measurement, material property, damping of the systems or component flow-rate. The reduced models are constructed such that all the parameters can be preserved with acceptable accuracy. Usually the time of simulating the reduced models is much shorter than directly simulating the original large system. However, the time of constructing the reduced model increases with the dimension of the original system. If the original system is very large, the process of obtaining the reduced model could become extremely slow. The recycling algorithm considered in this paper tries to accelerate the above process and reduce the time of deriving the reduced model to a reasonable range.
The method introduced here is from [1][2], and applies to a linear parametrized system, which has the following form in the frequency domain:
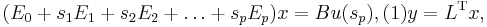
where 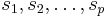 are the parameters of the system. They can be any scalar functions of some source parameters, like
are the parameters of the system. They can be any scalar functions of some source parameters, like 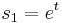 , where
, where 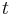 is time, or combination of several physical parameters like
is time, or combination of several physical parameters like 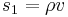 , where
, where  and
and  are two physical parameters.
are two physical parameters.
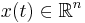 is the state vector,
is the state vector, 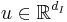 and
and 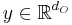 are, respectively, the inputs and outputs of the
system. To obtain the reduced model in (1), a
projection matrix
are, respectively, the inputs and outputs of the
system. To obtain the reduced model in (1), a
projection matrix  which is independent of all the parameters has
to be computed.
which is independent of all the parameters has
to be computed.
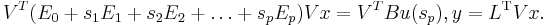
The matrix $V$ is derived by orthogonalizing a number of moment matrices of the system in (1)[1][2].
By defining 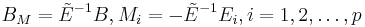 and
and
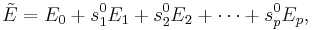
we can expand  in (1) at
in (1) at 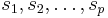 around a set of
expansion points
around a set of
expansion points ![p_0=[s_1^0,s_2^0,\cdots,s_p^0]](/morwiki/images/math/4/1/3/413a7d9006408a35467750f81e49d248.png) as below,
as below,
![x=[I-(\sigma_1M_1+\ldots +\sigma_pM_p]^{-1}B_Mu(s_p)
=\sum\limits_{i=0}^{\infty}(\sigma_1M_1+\ldots+\sigma_pM_p)^iB_Mu(s_p).](/morwiki/images/math/f/8/b/f8bf6e51fa587497870a6861474ec83c.png)
Here 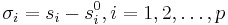 . We call the coefficients
in the above series expansion moment matrices of the parametrized
system, i.e. Failed to parse (lexing error): B_M, \ M_1B_M, \ \ldots, \ M_pB_M,\ M_1^2B_M, \ (M_1M_2+M_2M_1)B_M, \ \ldots, \ (M_1M_p+M_pM_1)B_M, \ M_p^2B_M, \ M_1^3B_M, \ \ldots
. The corresponding moments are those moment
matrices multiplied by
. We call the coefficients
in the above series expansion moment matrices of the parametrized
system, i.e. Failed to parse (lexing error): B_M, \ M_1B_M, \ \ldots, \ M_pB_M,\ M_1^2B_M, \ (M_1M_2+M_2M_1)B_M, \ \ldots, \ (M_1M_p+M_pM_1)B_M, \ M_p^2B_M, \ M_1^3B_M, \ \ldots
. The corresponding moments are those moment
matrices multiplied by  from the left. The matrix
from the left. The matrix  can be
generated by first explicitly computing some of the moment matrices
and then orthogonalizing them as is suggested in~\cite{Daniel04}.
The resulting $V$ is desired to expand the subspace:
can be
generated by first explicitly computing some of the moment matrices
and then orthogonalizing them as is suggested in~\cite{Daniel04}.
The resulting $V$ is desired to expand the subspace:
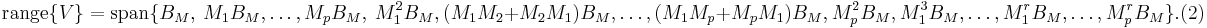
However,  does not really span the whole subspace, because the
latterly computed vectors in the subspace become linearly dependent
due to numerical instability. Therefore, with this matrix
does not really span the whole subspace, because the
latterly computed vectors in the subspace become linearly dependent
due to numerical instability. Therefore, with this matrix  one
cannot get an accurate reduced model which matches all the moments
included in the subspace.
one
cannot get an accurate reduced model which matches all the moments
included in the subspace.
Instead of directly computing the moment matrices in (2)[1], a
numerically robust method is proposed in [1] (the
detailed algorithm is described in [3]), which combines
the recursions in (4) with the modified Gram-Schmidt
process to implicitly compute the moment matrices. The computed  is actually an orthonormal basis of the subspace as below,
is actually an orthonormal basis of the subspace as below,
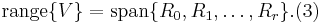
It can be proved that the subspace in~(2) is included in the
subspace in~(3). Due to the numerical stability properties of
the repeated modified Gram-Schmidt process employed in
[2][3], the reduced model derived from  in~(3) is computed in a numerically stable and accurate way.
in~(3) is computed in a numerically stable and accurate way.
![R_0=B_M, \ R_1=[M_1R_0,\ldots, M_pR_0],
R_2=[M_1R_1,\ldots, M_pR_1],
\vdots,
R_r=[M_1R_{r-1},\ldots, M_pR_{r-1}]
\vdots.](/morwiki/images/math/7/f/b/7fbc569d73839ffb50f99bc707354275.png)
Furthermore, one can see that each moment matrix is actually several
vectors multiplied by 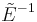 , and if the dimension of
, and if the dimension of
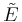 is very large, it is necessary to solve linear systems
like
is very large, it is necessary to solve linear systems
like
Failed to parse (unknown function "\label"): \label{sequence} \tilde{E}x=w_i, \ i=1,2,\ldots, l
to obtain 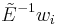 , where
, where 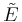 is generally
non-symmetric and
is generally
non-symmetric and 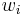 is a vector. Moreover, if quite a few of the
moment matrices need to be computed (this is normal when system
(1) contains more than 2 parameters), the number
is a vector. Moreover, if quite a few of the
moment matrices need to be computed (this is normal when system
(1) contains more than 2 parameters), the number 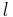 of
the linear systems in (\ref{sequence}) will be very large.
of
the linear systems in (\ref{sequence}) will be very large.
