Inverse Lyapunov Procedure

Description

The Inverse Lyapunov Procedure (ilp) is a synthetic random linear system generator. It is based on reversing the Balanced Truncation procedure and was developed in , where a description of the algorithm is given. In aggregate form, for randomly generated controllability and observability gramians, a balancing transformation is computed. The balanced gramian is the basis for an associated state-space system, which is determined by solving a Lyapunov equation and then unbalanced. A central point is the solution of the Lyapunov equations for the system matrix instead of the gramian matrix. This is feasable due to the symmetric (semi-)positive definiteness of the gramians and the requirement for a stable system, yet with a non-unique solution.

Implementation

An efficient approach to solving the Lyapunov equation is provided by empirical gramians.

Usage

Use the following matlab code to generate a random system as described above:

function [A B C] = ilp(J,N,O,s,r)
% ilp (inverse lyapunov procedure)
% by Christian Himpe, 2013--2018
% released under BSD 2-Clause License
%*
  if(nargin==5)
    rand('seed',r);
    randn('seed',r);
  end;

% Gramian Eigenvalues
  WC = exp(rand(N,1));
  WO = exp(rand(N,1));

% Gramian Eigenvectors
  [P,S,Q] = svd(randn(N));

% Balancing Transformation
  WC = P*diag(WC)*P';
  WO = Q*diag(WO)*Q';
  [U,D,V] = svd(WC*WO);

% Input and Output
  B = randn(N,J);

  if(nargin>=4 && s~=0)
    C = B';
  else
    C = randn(O,N);
  end

% Scale Output Matrix
  BB = sum(B.*B,2);  % = diag(B*B')
  CC = sum(C.*C,1)'; % = diag(C'*C)
  C = bsxfun(@times,C,sqrt(BB./CC)');

% Solve System Matrix
  A = -sylvester(D,D,B*B');

% Unbalance System
  A = V*A*U';
  B = V*B;
  C = C*U';

end

The function call requires three parameters; the number of inputs 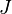$J$, of states $N$ and outputs 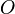$O$. Optionally, a symmetric system can be enforced with the parameter $s \neq 0$. For reproducibility, the random number generator seed can be controlled by the parameter $r \in \mathbb{N}$. The return value consists of three matrices; the system matrix $A$, the input matrix $B$ and the output matrix $C$.

[A,B,C] = ilp(J,N,O,s,r);

Contact

Christian Himpe