m (Added curly bracket with system name.) |
|||
| Line 11: | Line 11: | ||
Consider the standard linear-time invariant system |
Consider the standard linear-time invariant system |
||
| − | ::<math>\begin{align} \dot{x}(t) & = Ax(t) + Bu(t),\\ y(t) & = Cx(t) + Du(t), \end{align}</math> |
+ | ::<math>G:\left\{ \begin{align} \dot{x}(t) & = Ax(t) + Bu(t),\\ y(t) & = Cx(t) + Du(t), \end{align} \right.</math> |
with the matrices <math style="vertical-align: top;">A \in \mathbb{R}^{n \times n}</math>, <math style="vertical-align: top;">B \in \mathbb{R}^{n \times m}</math>, <math style="vertical-align: top;">C \in \mathbb{R}^{p \times n}</math> and <math style="vertical-align: top;">D \in \mathbb{R}^{p \times m}</math>. |
with the matrices <math style="vertical-align: top;">A \in \mathbb{R}^{n \times n}</math>, <math style="vertical-align: top;">B \in \mathbb{R}^{n \times m}</math>, <math style="vertical-align: top;">C \in \mathbb{R}^{p \times n}</math> and <math style="vertical-align: top;">D \in \mathbb{R}^{p \times m}</math>. |
||
Revision as of 16:37, 5 January 2018
The Hankel-norm approximation method is a model reduction approach that solves the best-approximation problem in the Hankel semi-norm[1].
Description
Consider the standard linear-time invariant system
- \[G:\left\{ \begin{align} \dot{x}(t) & = Ax(t) + Bu(t),\\ y(t) & = Cx(t) + Du(t), \end{align} \right.\]
with the matrices 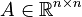 ,
, 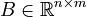 ,
, 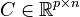 and
and 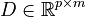 .
For a system
.
For a system 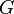 , the Hankel operator
, the Hankel operator 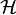 maps past inputs \(u_{-}\) to future outputs \(y_{+}\) of the system, i.e., \(y_{+} = \mathcal{H}u_{-}\).
Then, the Hankel semi-norm of the system \(G\) is defined as the \(\mathcal{L}_{2}\)-induced norm of the Hankel opertor
maps past inputs \(u_{-}\) to future outputs \(y_{+}\) of the system, i.e., \(y_{+} = \mathcal{H}u_{-}\).
Then, the Hankel semi-norm of the system \(G\) is defined as the \(\mathcal{L}_{2}\)-induced norm of the Hankel opertor
- \[\lVert G \rVert_{H} := \sup\limits_{u_{-} \in \mathcal{L}_{2}\left(-\infty, 0\right]}\frac{\lVert y_{+} \rVert_{\mathcal{L}_{2}}}{\lVert u_{-} \rVert_{\mathcal{L}_{2}}}.\]
If the system \(G\) is stable, the controllability and observability Gramians \(\mathcal{G}_{c}\) and \(\mathcal{G}_{o}\) of the system above are given as the unique positive semidefinite solutions of the two Lyapunov equations
- \[\begin{align} A\mathcal{G}_{c} + \mathcal{G}_{c}A^{T} + BB^{T} & = 0,\\ A^{T}\mathcal{G}_{o} + \mathcal{G}_{o}A + C^{T}C & = 0. \end{align}\]
The Hankel singular values of the system \(G\) are then defined as the square-roots of the eigenvalues of the multiplied system Gramians, i.e., \(\sqrt{\Lambda(\mathcal{G}_{c}\mathcal{G}_{o})} = \{ \varsigma_{1}, \ldots, \varsigma_{n} \}\). It can be shown, that the Hankel semi-norm of a system is given by the largest Hankel singular value \(\lVert G \rVert_{H} = \varsigma_{\text{max}}\).
The idea of the Hankel-norm approximation method is, to construct a reduced-order model \(G_{r}\) of order \(r\) such that the error system \(\mathcal{E} = G - G_{r}\) has a scaled all-pass transfer function
- \[\mathcal{E}(s)\mathcal{E}^{T}(-s) = \varsigma_{r + 1}^{2} I_{p},\]
with \(\varsigma_{r + 1}\) the \((r + 1)\)-st Hankel singular value of the system \(G\).
For such error systems, the Hankel semi-norm is known to be \(\lVert \mathcal{E} \rVert_{H} = \varsigma_{r + 1}.\)
Algorithm
Here, the algorithm of the Hankel-norm approximation method is shortly described [2]:
1. Compute a minimal balanced realization \((\check{A}, \check{B}, \check{C}, D)\) using the balanced truncation square-root method.
2. Choose the Hankel singular value \(\varsigma_{r + 1}\).
3. Permute the balanced realization such that the Gramians have the form
\(\begin{align}\check{\mathcal{G}}_{c} = \check{\mathcal{G}}_{o} & = \mathrm{diag}(\varsigma_{1}, \ldots, \varsigma_{r}, \varsigma_{r + k + 1}, \ldots, \varsigma_{n}, \varsigma_{r + 1}I_{k})\\ & = \mathrm{diag}(\Sigma, \varsigma_{r + 1}I_{k}).\end{align}\)
4. Partition the resulting permuted system according to the Gramians
\(\check{A} = \begin{bmatrix} A_{11} & A_{12}\\ A_{21} & A_{22}\end{bmatrix}, ~~~ \check{B} = \begin{bmatrix} B_{1}\\ B_{2}\end{bmatrix}, \check{C} = \begin{bmatrix} C_{1} & C_{2}\end{bmatrix},\)
where \(A_{22} \in \mathbb{R}^{k \times k}\), \(B_{2} \in \mathbb{R}^{k \times m}\) and \(C_{2} \in \mathbb{R}^{p \times k}\).
5. Compute the transformation
\(\begin{align}\tilde{A} & = \Gamma^{-1}(\varsigma_{r+1}^{2}A_{11}^{T} + \Sigma A_{11} \Sigma + \varsigma_{r+1}C_{1}^{T}UB_{1}^{T}),\\ \tilde{B} & = \Gamma^{-1}(\Sigma B_{1} - \varsigma_{r+1}C_{1}^{T}U),\\ \tilde{C} & = C_{1}\Sigma - \varsigma_{r+1}UB_{1}^{T},\\ \tilde{D} & = D + \varsigma_{r+1}U,\end{align}\)
with \(U = \left(C_{2}^{T}\right)^{\dagger}B_{2}\) and \(\Gamma = \Sigma^{2} - \varsigma_{r+1}^{2}I_{n-k}\).
6. Compute the additive decomposition
\(\tilde{G}(s) = \tilde{C}(sI_{n-k} - \tilde{A})^{-1}\tilde{B} + \tilde{D} = G_{r}(s) + F(s),\)
where \(F\) is anti-stable and \(G_{r}\) is the \(r\)-th order stable Hankel-norm approximation.
References
- ↑ K. Glover. All optimal Hankel-norm approximations of linear multivariable systems and their
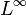 -error norms. Internat. J. Control, 39(6):1115-1193, 1984.
-error norms. Internat. J. Control, 39(6):1115-1193, 1984.
- ↑ P. Benner, E. S. Quintana-Ortí, and G. Quintana-Ortí. Computing optimal Hankel norm approximations of large-scale systems. In 2004 43rd IEEE Conference on Decision and Control (CDC), volume 3, pages 3078-3083, Atlantis, Paradise Island, Bahamas, December 2004. Institute of Electrical and Electronics Engineers.
