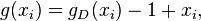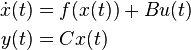(→Data: Fixes based on comments by Maria) |
(Added Dimensions and Citaiton section, more references and some fixes.) |
||
| Line 6: | Line 6: | ||
==Description== |
==Description== |
||
| + | The nonlinear RC-ladder is an electronic test circuit introduced in <ref name="chen99"/>. |
||
| ⚫ | |||
| − | This nonlinear first-order system models a resistor-capacitor network that exhibits a distinct nonlinear |
+ | This nonlinear first-order system models a resistor-capacitor network that exhibits a distinct nonlinear behavior caused by the nonlinear resistors consisting of a parallel connected resistor with a diode. |
<figure id="fig:nrcl">[[File:nrcl.png|400px|thumb|right| Nonlinear RC-Ladder]]</figure> |
<figure id="fig:nrcl">[[File:nrcl.png|400px|thumb|right| Nonlinear RC-Ladder]]</figure> |
||
| − | ==Model== |
+ | ===Model=== |
| − | The underlying model is given by a ([[List_of_abbreviations#SISO|SISO]]) gradient system of the form<ref |
+ | The underlying model is given by a ([[List_of_abbreviations#SISO|SISO]]) gradient system of the form <ref name="condon04"/>: |
:<math> |
:<math> |
||
| Line 24: | Line 24: | ||
</math> |
</math> |
||
| − | where the |
+ | where the <math>g</math> is a mapping <math>g(x):\mathbb{R} \to \mathbb{R}</math>: |
| + | |||
:<math> |
:<math> |
||
| − | g( |
+ | g(x_i) = g_D(x_i) -1 + x_i, |
</math> |
</math> |
||
| + | which combines the effect of a [[wikipedia:Diode|diode]] and a resistor. |
||
| ⚫ | |||
| + | |||
| + | ===Nonlinearity=== |
||
| + | The nonlinearity <math>g_S</math> models a diode as a nonlinear resistor, |
||
| + | based on the [[wikipedia:Diode_modelling#Shockley_diode_model|Shockley model]] <ref name="reis14"/>: |
||
| + | |||
| + | :<math> |
||
| + | g_D(x_i) = i_S (\exp(u_P x_i) - 1), |
||
| + | </math> |
||
| + | |||
| + | with material parameters <math>i_S > 0</math> and <math>u_P > 0</math>. |
||
| + | |||
| + | For this benchmark the parameters are selected as: <math>i_S = 1</math> and <math>u_P = 40</math> as in <ref name="chen99"/>. |
||
| + | |||
| + | |||
| ⚫ | |||
| − | As external input several alternatives are presented in<ref |
+ | As external input several alternatives are presented in <ref name="chen00"/>, which are listed next. |
A simple step function is given by: |
A simple step function is given by: |
||
:<math> |
:<math> |
||
| Line 42: | Line 58: | ||
</math> |
</math> |
||
| − | Additional input sources are given by conjunction of sine waves with different periods: |
+ | Additional input sources are given by conjunction of sine waves with different periods <ref name="condon04a"/>: |
:<math> |
:<math> |
||
u_3(t) = \sin(2\pi 50t)+\sin(2\pi 1000t), |
u_3(t) = \sin(2\pi 50t)+\sin(2\pi 1000t), |
||
| Line 50: | Line 66: | ||
u_4(t) = \sin(2\pi 50t) \sin(2\pi 1000t). |
u_4(t) = \sin(2\pi 50t) \sin(2\pi 1000t). |
||
</math> |
</math> |
||
| − | |||
==Data== |
==Data== |
||
| − | A sample procedural MATLAB implementation of order N is given by: |
+ | A sample procedural MATLAB implementation of order <math>N</math> is given by: |
<div class="thumbinner" style="width:540px;text-align:left;"> |
<div class="thumbinner" style="width:540px;text-align:left;"> |
||
<source lang="matlab"> |
<source lang="matlab"> |
||
| + | function [f,B,C] = nrc(N) |
||
%% Procedural generation of "Nonlinear RC Ladder" benchmark system |
%% Procedural generation of "Nonlinear RC Ladder" benchmark system |
||
| − | % nonlinearity |
+ | % nonlinearity |
| − | g = @(x) exp(40.0*x) + x - 1.0; |
+ | g = @(x) exp(40.0*x) + x - 1.0; |
| − | A0 = sparse(N,N); |
+ | A0 = sparse(N,N); |
| − | A0(1,1) = 1; |
+ | A0(1,1) = 1; |
| − | A1 = spdiags(ones(N-1,1),-1,N,N) - speye(N); |
+ | A1 = spdiags(ones(N-1,1),-1,N,N) - speye(N); |
| − | A1(1,1) = 0; |
+ | A1(1,1) = 0; |
| − | A2 = spdiags([ones(N-1,1);0],0,N,N) - spdiags(ones(N,1),1,N,N); |
+ | A2 = spdiags([ones(N-1,1);0],0,N,N) - spdiags(ones(N,1),1,N,N); |
| − | % input matrix |
+ | % input matrix |
| − | B = sparse(N,1); |
+ | B = sparse(N,1); |
| − | B(1,1) = 1; |
+ | B(1,1) = 1; |
| − | % output matrix |
+ | % output matrix |
| − | C = sparse(1,N); |
+ | C = sparse(1,N); |
| − | C(1,1) = 1; |
+ | C(1,1) = 1; |
| + | |||
| ⚫ | |||
| ⚫ | |||
| + | |||
| + | end |
||
| ⚫ | |||
| ⚫ | |||
| − | y = @(x) C*x; |
||
</source> |
</source> |
||
</div> |
</div> |
||
| + | |||
| + | Here the nonlinear part of the vectorfield is realized in a vectorized form as a [[wikipedia:Closure_(computer_programming)|closure]]. |
||
| + | |||
| + | ==Dimensions== |
||
| + | |||
| + | System structure: |
||
| + | :<math> |
||
| + | \begin{align} |
||
| + | \dot{x}(t) &= f(x(t)) + Bu(t) \\ |
||
| + | y(t) &= Cx(t) |
||
| + | \end{align} |
||
| + | </math> |
||
| + | |||
| + | System dimensions: |
||
| + | |||
| + | <math>f : \mathbb{R}^N \to \mathbb{R}^N</math>, |
||
| + | <math>B \in \mathbb{R}^{N \times 1}</math>, |
||
| + | <math>C \in \mathbb{R}^{1 \times N}</math>. |
||
| + | |||
| + | ==Citation== |
||
| + | |||
| + | To cite this benchmark, use the following references: |
||
| + | |||
| + | * For the benchmark itself and its data: |
||
| + | ::The MORwiki Community. '''Nonlinear RC Ladder'''. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Nonlinear_RC_Ladder |
||
| + | |||
| + | @MISC{morwiki_modgyro, |
||
| + | author = {The {MORwiki} Community}, |
||
| + | title = {Nonlinear RC Ladder}, |
||
| + | howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
||
| + | url = {<nowiki>http://modelreduction.org/index.php/Nonlinear_RC_Ladder</nowiki>}, |
||
| + | year = {2018} |
||
| + | } |
||
| + | |||
| + | * For the background on the benchmark: <span class="plainlinks">[https://morwiki.mpi-magdeburg.mpg.de/BibTeX/#morChe99 morChe99]</span> (<span class="plainlinks">[https://morwiki.mpi-magdeburg.mpg.de/BibTeX/html/mor_bib.html#morChe99 BibTeX]</span>) |
||
==References== |
==References== |
||
| − | <references |
+ | <references> |
| + | |||
| + | <ref name="chen99">Y. Chen, "<span class="plainlinks">[http://hdl.handle.net/1721.1/9381 Model Reduction for Nonlinear Systems]</span>", Master Thesis, 1999.</ref> |
||
| + | |||
| ⚫ | <ref name="chen00">Y. Chen and J. White, "<span class="plainlinks">[http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.19.8951&rep=rep1&type=pdf A quadratic method for nonlinear model order reduction]</span>", Int. conference on modelling and simulation of Microsystems semiconductors, sensors and actuators, 2000.</ref> |
||
| + | |||
| + | <ref name="condon04">M. Condon and R. Ivanov, "<span class="plainlinks">[https://doi.org/10.1007/s00332-004-0617-5 Empirical balanced truncation for nonlinear systems]</span>", Journal of Nonlinear Science 14(5):405--414, 2004.</ref> |
||
| + | |||
| + | <ref name="condon04a">M. Condon and R. Ivanov, "<span class="plainlinks">[https://doi.org/10.1108/03321640410510730 Model Reduction of Nonlinear Systems]</span>", COMPEL 23(2): 547--557, 2004</ref> |
||
| + | |||
| + | <ref name="reis14">T. Reis. "<span class="plainlinks">[https://doi.org/10.1007/978-3-319-08437-4_2 Mathematical Modeling and Analysis of Nonlinear Time-Invariant RLC Circuits]</span>", In: Large-Scale Networks in Engineering and Life Sciences. Modeling and Simulation in Science, Engineering and Technology: 125--198, 2014.</ref> |
||
| + | |||
| + | </references> |
||
==Contact== |
==Contact== |
||
Revision as of 10:02, 8 March 2018
Description
The nonlinear RC-ladder is an electronic test circuit introduced in [1]. This nonlinear first-order system models a resistor-capacitor network that exhibits a distinct nonlinear behavior caused by the nonlinear resistors consisting of a parallel connected resistor with a diode.
Model
The underlying model is given by a (SISO) gradient system of the form [2]:
where the  is a mapping
is a mapping 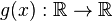 :
:
which combines the effect of a diode and a resistor.
Nonlinearity
The nonlinearity 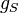 models a diode as a nonlinear resistor,
based on the Shockley model [3]:
models a diode as a nonlinear resistor,
based on the Shockley model [3]:
with material parameters  and
and  .
.
For this benchmark the parameters are selected as:  and
and  as in [1].
as in [1].
Input
As external input several alternatives are presented in [4], which are listed next. A simple step function is given by:
an exponential decaying input is provided by:
Additional input sources are given by conjunction of sine waves with different periods [5]:
Data
A sample procedural MATLAB implementation of order  is given by:
is given by:
function [f,B,C] = nrc(N)
%% Procedural generation of "Nonlinear RC Ladder" benchmark system
% nonlinearity
g = @(x) exp(40.0*x) + x - 1.0;
A0 = sparse(N,N);
A0(1,1) = 1;
A1 = spdiags(ones(N-1,1),-1,N,N) - speye(N);
A1(1,1) = 0;
A2 = spdiags([ones(N-1,1);0],0,N,N) - spdiags(ones(N,1),1,N,N);
% input matrix
B = sparse(N,1);
B(1,1) = 1;
% output matrix
C = sparse(1,N);
C(1,1) = 1;
% vector field and output functional
f = @(x) -g(A0*x) + g(A1*x) - g(A2*x);
end
Here the nonlinear part of the vectorfield is realized in a vectorized form as a closure.
Dimensions
System structure:
System dimensions:
 ,
,
 ,
,
 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community. Nonlinear RC Ladder. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Nonlinear_RC_Ladder
@MISC{morwiki_modgyro,
author = {The {MORwiki} Community},
title = {Nonlinear RC Ladder},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/Nonlinear_RC_Ladder},
year = {2018}
}
References
- ↑ 1.0 1.1 Y. Chen, "Model Reduction for Nonlinear Systems", Master Thesis, 1999.
- ↑ M. Condon and R. Ivanov, "Empirical balanced truncation for nonlinear systems", Journal of Nonlinear Science 14(5):405--414, 2004.
- ↑ T. Reis. "Mathematical Modeling and Analysis of Nonlinear Time-Invariant RLC Circuits", In: Large-Scale Networks in Engineering and Life Sciences. Modeling and Simulation in Science, Engineering and Technology: 125--198, 2014.
- ↑ Y. Chen and J. White, "A quadratic method for nonlinear model order reduction", Int. conference on modelling and simulation of Microsystems semiconductors, sensors and actuators, 2000.
- ↑ M. Condon and R. Ivanov, "Model Reduction of Nonlinear Systems", COMPEL 23(2): 547--557, 2004