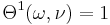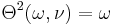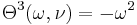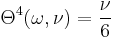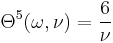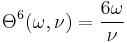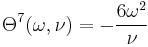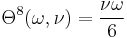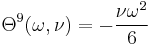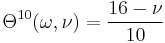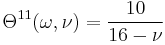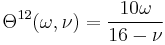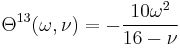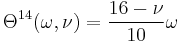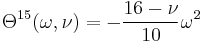m (link to matrices corrected) |
(Updated Coplanar Waveguide) |
||
| Line 11: | Line 11: | ||
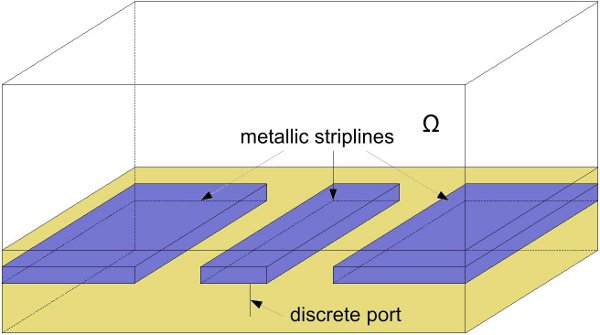
A '''coplanar waveguide''' (see <xr id="fig:coplanar"/>) is a microwave semiconductor device, which is governed by maxwell's equations. |
A '''coplanar waveguide''' (see <xr id="fig:coplanar"/>) is a microwave semiconductor device, which is governed by maxwell's equations. |
||
| − | The '''coplanar waveguide''' considered with dielectric overlay, i.e. a transmission line shielded within two layers of multilayer board with 0.5mm thickness are buried in a substrate with 10mm thickness and relative permittivity |
+ | The '''coplanar waveguide''' considered with dielectric overlay, i.e. a transmission line shielded within two layers of multilayer board with <math>0.5mm</math> thickness are buried in a substrate with <math>10mm</math> thickness and relative permittivity |
| − | <math> |
+ | <math>\epsilon_r = 4.4 </math> and relative permeability <math>\mu_r = 1 </math>, and low conductivity <math>\sigma = 0.02 S/m </math>. |
| + | The low-loss upper layer has low permittivity <math>\epsilon_r = 1.07 </math> and <math>\sigma = 0.01 S/m</math>. |
||
| − | <math> \sigma = 0.01 S/m </math>. The whole structure is enlosed in a metallic box of dimension 140mm by 100mm by 50mm. The discrete port with 50ohm lumped load imposes 1 A current as the input to the one side of the strip. The voltage along the discrete port 2 at the end of the other side of coupled lines is integrated as the output. |
||
| + | The whole structure is enlosed in a metallic box of dimension <math>140mm</math> by <math>100mm</math> by <math>50mm</math>. |
||
| + | The discrete port with <math>50Ohm</math> lumped load imposes <math>1 A</math> current as the input to the one side of the strip. |
||
| + | The voltage along the discrete port 2 at the end of the other side of coupled lines is integrated as the output. |
||
<figure id="fig:coplanar"> |
<figure id="fig:coplanar"> |
||
| − | [[File:CoplanarWaveguideScaled.jpg|frame|<caption>Coplanar Waveguide Model<ref |
+ | [[File:CoplanarWaveguideScaled.jpg|frame|<caption>Coplanar Waveguide Model<ref name="hess2003"/></caption>]] |
</figure> |
</figure> |
||
| Line 31: | Line 34: | ||
appearance in the summation. |
appearance in the summation. |
||
| ⚫ | |||
| ⚫ | |||
| − | |||
| − | |||
| ⚫ | |||
:<math> \Theta^1(\omega, \nu) = 1 </math> |
:<math> \Theta^1(\omega, \nu) = 1 </math> |
||
| Line 66: | Line 66: | ||
:<math> \Theta^{15}(\omega, \nu) = -\frac{16 - \nu}{10} \omega^2 </math> |
:<math> \Theta^{15}(\omega, \nu) = -\frac{16 - \nu}{10} \omega^2 </math> |
||
| − | The parameter domain of interest is <math> |
+ | The parameter domain of interest is <math>\omega \in [0.6, 3.0] * 10^9 </math> Hz, where the factor of <math>10^9 </math> has already been taken into account |
| − | while assembling the matrices, while the geometric variation occurs between <math> \nu \in [2.0, 14.0] |
+ | while assembling the matrices, while the geometric variation occurs between <math> \nu \in [2.0, 14.0]</math>. |
| + | The input functional also has a factor of <math> \omega </math>. |
||
| − | There are two output functionals, which is due to the fact, that the complex system has been rewritten as a real symmetric one. |
+ | There are two output functionals, which is due to the fact, that the complex system has been rewritten as a real symmetric one. |
| + | In particular the computation of the output |
||
| − | <math> |
+ | <math>s(u) = | l^T * u |</math> with complex vector <math>u</math> turns into <math>s(u) = \sqrt{ (l_1^T * u)^2 + (l_2^T * u)^2 }</math> with real vector <math> u </math>. |
==Origin== |
==Origin== |
||
| − | The models have been developed within the [http://www.moresim4nano.org MoreSim4Nano project |
+ | The models have been developed within the [http://www.moresim4nano.org MoreSim4Nano] project. |
| + | |||
| + | ==Data== |
||
| + | |||
| ⚫ | |||
==References== |
==References== |
||
| − | <references |
+ | <references> |
| + | |||
| + | <ref name="hess2003">M.W. Hess, P. Benner, "<span class="plainlinks">[https://doi.org/10.1109/TMTT.2013.2258167 Fast Evaluation of Time-Harmonic Maxwell's Equations Using the Reduced Basis Method]</span>", IEEE Transactions on Microwave Theory and Techniques, 61(6): 2265--2274, 2013.</ref> |
||
| + | |||
| + | </references> |
||
==Contact== |
==Contact== |
||
Revision as of 10:21, 28 February 2018
Description
A coplanar waveguide (see xx--CrossReference--dft--fig:coplanar--xx) is a microwave semiconductor device, which is governed by maxwell's equations.
The coplanar waveguide considered with dielectric overlay, i.e. a transmission line shielded within two layers of multilayer board with 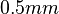 thickness are buried in a substrate with
thickness are buried in a substrate with 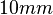 thickness and relative permittivity
thickness and relative permittivity
 and relative permeability
and relative permeability  , and low conductivity
, and low conductivity 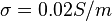 .
The low-loss upper layer has low permittivity
.
The low-loss upper layer has low permittivity  and
and 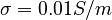 .
The whole structure is enlosed in a metallic box of dimension
.
The whole structure is enlosed in a metallic box of dimension 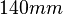 by
by 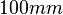 by
by 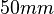 .
The discrete port with
.
The discrete port with 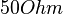 lumped load imposes
lumped load imposes 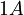 current as the input to the one side of the strip.
The voltage along the discrete port 2 at the end of the other side of coupled lines is integrated as the output.
current as the input to the one side of the strip.
The voltage along the discrete port 2 at the end of the other side of coupled lines is integrated as the output.
Data
Considered parameters are the frequency  and the width
and the width  of the middle stripline.
of the middle stripline.
The affine form  can be established using
can be established using  affine terms.
affine terms.
The discretized bilinear form is  , with matrices
, with matrices  .
.
The matrices corresponding to the bilinear forms  as well as the input and output forms and H(curl) inner product matrix have been assembled
using the Finite Element Method, resulting in 7754 degrees of freedom, after removal of boundary conditions. The files are numbered according to their
appearance in the summation.
as well as the input and output forms and H(curl) inner product matrix have been assembled
using the Finite Element Method, resulting in 7754 degrees of freedom, after removal of boundary conditions. The files are numbered according to their
appearance in the summation.
The coefficient functions are given by:
The parameter domain of interest is ![\omega \in [0.6, 3.0] * 10^9](/morwiki/images/math/0/a/4/0a47dfe123bc72ced89d668c0bcbdf68.png) Hz, where the factor of
Hz, where the factor of  has already been taken into account
while assembling the matrices, while the geometric variation occurs between
has already been taken into account
while assembling the matrices, while the geometric variation occurs between ![\nu \in [2.0, 14.0]](/morwiki/images/math/7/5/6/756a434dfb914a085ee3854e8accd924.png) .
The input functional also has a factor of
.
The input functional also has a factor of  .
.
There are two output functionals, which is due to the fact, that the complex system has been rewritten as a real symmetric one. In particular the computation of the output
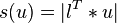 with complex vector
with complex vector  turns into
turns into 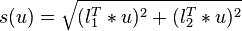 with real vector
with real vector  .
.
Origin
The models have been developed within the MoreSim4Nano project.
Data
The files are numbered according to their appearance in the summation and can be found here: Matrices_cp.tar.gz.
References
- ↑ M.W. Hess, P. Benner, "Fast Evaluation of Time-Harmonic Maxwell's Equations Using the Reduced Basis Method", IEEE Transactions on Microwave Theory and Techniques, 61(6): 2265--2274, 2013.