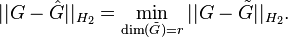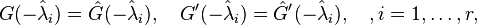Difference between revisions of "Iterative Rational Krylov Algorithm"

Revision as of 09:14, 30 May 2013

Description

The iterative rational Krylov algorithm (IRKA) is an interpolation-based model reduction method for single-input-single-output linear time invariant systems

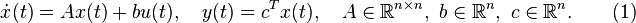\dot{x}(t)=A x(t)+b u(t), \quad y(t)=c^Tx(t),\quad A\in\mathbb{R}^{n\times n},~b\in\mathbb{R}^{n},~c\in\mathbb{R}^{n}.\qquad (1)

(1)

For a given system 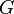$G$ and a prescribed reduced system order $r$ , the goal of the algorithm is to find a local minimizer 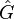$\hat{G}$ for the 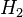$H_2$ model reduction problem

||G-\hat{G} ||_{H_2} = \min_{\text{dim}(\tilde{G})=r} ||G-\tilde{G}||_{H_2}.

Initially investigated in ^[1], first order necessary conditions for a local minimizer 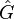$\hat{G}$ imply that its rational transfer function 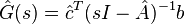$\hat{G}(s)=\hat{c}^T (sI-\hat{A})^{-1}b$ is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,

G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r,

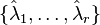where $\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\}$ are assumed to be the simple poles of 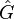$\hat{G}$ . Based on the idea of rational interpolation by rational Krylov subspaces, in ^[2] the authors have picked up the optimality conditions and proposed to iteratively correct projection subspaces until interpolation at the reflected reduced system poles is ensured. In pseudocode, the classical algorithm (IRKA) from ^[2] looks like

1. Make an initial selection of  $\sigma_i$  for  $i=1,\dots,r$  that is closed under conjugation and fix a convergence tolerance  $tol$ .
2. Choose  $V_r$  and  $W_r$  so that  $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$ ,  $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \}$  and  $W_r^TV_r=I$ .
3. while (relative change in  $\{\sigma_i\} > tol$ )
 (a)  $\hat{A} = W_r^TAV_r$ 
 (b) Assign  $\sigma_i \leftarrow -\lambda_i(\hat{A}),$  for  $i=1,\dots,r$ 
 (c) Update  $V_r$  and  $W_r$  so that  $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$ ,  $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \}$  and  $W_r^TV_r=I$ .
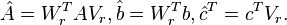
4.  $\hat{A} = W_r^TAV_r, \hat{b}= W_r^Tb, \hat{c}^T = c^TV_r.$

Although a rigorous convergence proof so far has only be given for symmetric state space systems ^[3], numerous experiments have shown that the algorithm often converges rapidly. Moreover, the algorithm has been extended to, e.g., multiple-input-multiple output, discrete time and differential algebraic systems.

References

^[1]

^[2]

^[3]

</ references>

↑ ^1.0 ^1.1 L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588, 1967.
↑ ^2.0 ^2.1 ^2.2 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638, 2008.
↑ ^3.0 ^3.1 G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691, 2012.

[MeiL67-1] 1.0 ^1.1 L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588, 1967.

[GugAB08-2] 2.0 ^2.1 ^2.2 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638, 2008.

[FlaBG12-3] 3.0 ^3.1 G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691, 2012.

[1]

[2]

[3]

@@ Line 43: / Line 43: @@
 <references>
-<ref name="MeiL67"> L. Meier, D.G. Luenberger, "<span class="plainlinks">[http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1098680&tag=1 Approximation of linear constant systems]</span>", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588 1967</ref>
+<ref name="MeiL67"> L. Meier, D.G. Luenberger, "<span class="plainlinks">[http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1098680&tag=1 Approximation of linear constant systems]</span>", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588, 1967.</ref>
-<ref name="GugAB08"> S. Gugercin, A.C. Antoulas, C. Beattie "<span class="plainlinks">[http://epubs.siam.org/doi/abs/10.1137/060666123 H2 Model Reduction for Large-Scale Linear Dynamical Systems]</span>", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638 2008</ref>
+<ref name="GugAB08"> S. Gugercin, A.C. Antoulas, C. Beattie "<span class="plainlinks">[http://epubs.siam.org/doi/abs/10.1137/060666123 H2 Model Reduction for Large-Scale Linear Dynamical Systems]</span>", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638, 2008.</ref>
-<ref name="FlaBG12"> G. Flagg, C. Beattie, S. Gugercin "<span class="plainlinks">[http://www.sciencedirect.com/science/article/pii/S0167691112000576 Convergence of the Iterative Rational Krylov Algorithm]</span>", Systems & Control Letters, vol.61, no.6, pp.688-691 2012</ref>
+<ref name="FlaBG12"> G. Flagg, C. Beattie, S. Gugercin "<span class="plainlinks">[http://www.sciencedirect.com/science/article/pii/S0167691112000576 Convergence of the Iterative Rational Krylov Algorithm]</span>", Systems & Control Letters, vol.61, no.6, pp.688-691, 2012.</ref>
 </ references>