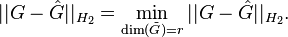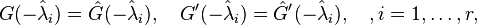Difference between revisions of "Iterative Rational Krylov Algorithm"

Revision as of 09:09, 30 May 2013

Description

The iterative rational Krylov algorithm (IRKA) is an interpolation-based model reduction method for single-input-single-output linear time invariant systems

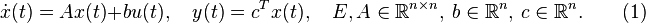\dot{x}(t)=A x(t)+b u(t), \quad y(t)=c^Tx(t),\quad E,A\in\mathbb{R}^{n\times n},~b\in\mathbb{R}^{n},~c\in\mathbb{R}^{n}.\qquad (1)

(1)

For a given system 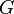$G$ and a prescribed reduced system order $r$ , the goal of the algorithm is to find a local minimizer 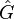$\hat{G}$ for the 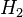$H_2$ model reduction problem

||G-\hat{G} ||_{H_2} = \min_{\text{dim}(\tilde{G})=r} ||G-\hat{G}||_{H_2}.

Initially investigated in ^[1], first order necessary conditions for a local minimizer 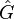$\hat{G}$ imply that its rational transfer function 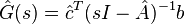$\hat{G}(s)=\hat{c}^T (sI-\hat{A})^{-1}b$ is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,

G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r,

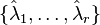where $\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\}$ are assumed to be the simple poles of $\hat{G}$ . Based on the idea of rational interpolation by rational Krylov subspaces, in ^[2] the authors have picked up the optimality conditions and proposed to iteratively correct the projection subspaces. In pseudocode, the classical algorithm (IRKA) from ^[2] looks like

1. Make an initial selection of  $\sigma_i$  for  $i=1,\dots,r$  that is closed under conjugation and fix a convergence tolerance  $tol$ .
2. Choose  $V_r$  and  $W_r$  so that  $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$ ,  $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \}$  and  $W_r^TV_r=I$ .
3. while (relative change in  $\{\sigma_i\} > tol$ )
 (a)  $\hat{A} = W_r^TAV_r$ 
 (b) Assign  $\sigma_i \leftarrow -\lambda_i(\hat{A}),$  for  $i=1,\dots,r$ 
 (c) Update  $V_r$  and  $W_r$  so that  $\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \}$ ,  $\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \}$  and  $W_r^TV_r=I$ .
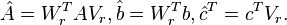
4.  $\hat{A} = W_r^TAV_r, \hat{b}= W_r^Tb, \hat{c}^T = c^TV_r.$

Although a rigorous convergence proof so far has only be given for symmetric state space systems ^[3], numerous experiments have shown that the algorithm often converges rapidly.

References

^[1]

^[2]

^[3]

</ references>

↑ ^1.0 ^1.1 L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588 1967
↑ ^2.0 ^2.1 ^2.2 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638 2008
↑ ^3.0 ^3.1 G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691 2012

[MeiL67-1] 1.0 ^1.1 L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588 1967

[GugAB08-2] 2.0 ^2.1 ^2.2 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638 2008

[FlaBG12-3] 3.0 ^3.1 G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691 2012

[1]

[2]

[3]

@@ Line 27: / Line 27: @@
 G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r,
 </math>
-where <math>\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\} </math> are assumed to be the single poles of <math> \hat{G} </math>. Based on the idea of rational interpolation by rational Krylov subspaces, in <ref name="GugAB08"></ref> the authors have picked up the optimality conditions and proposed to iteratively correct the projection subspaces. In pseudocode, the classical algorithm (IRKA) from <ref name="GugAB08"></ref> looks like
+where <math>\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\} </math> are assumed to be the simple poles of <math> \hat{G} </math>. Based on the idea of rational interpolation by rational Krylov subspaces, in <ref name="GugAB08"></ref> the authors have picked up the optimality conditions and proposed to iteratively correct the projection subspaces. In pseudocode, the classical algorithm (IRKA) from <ref name="GugAB08"></ref> looks like
 . Make an initial selection of <math>\sigma_i </math> for <math>i=1,\dots,r </math> that is closed under conjugation and fix a convergence tolerance <math>tol</math>.