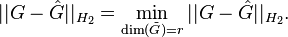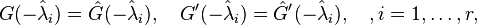| Line 6: | Line 6: | ||
==Description== |
==Description== |
||
| + | |||
| + | The iterative rational Krylov algorithm (IRKA) is an interpolation-based model reduction method for single-input-single-output linear time systems |
||
| + | |||
| + | :<equation id="gensys" shownumber> |
||
| + | <math> |
||
| + | E\dot{x}(t)=A x(t)+b u(t), \quad |
||
| + | y(t)=c^Tx(t),\quad E,A\in\mathbb{R}^{n\times n},~b\in\mathbb{R}^{n},~c\in\mathbb{R}^{n}.\qquad (1) |
||
| + | </math> |
||
| + | </equation> |
||
| + | |||
| + | For a given system <math>G </math> and a prescribed reduced system order <math>r</math>, the goal of the algorithm is to find a local minimizer <math>\hat{G} </math> for the <math> H_2 </math> model reduction problem |
||
| + | |||
| + | :<math> |
||
| + | ||G-\hat{G} ||_{H_2} = \min_{\text{dim}(\tilde{G})=r} ||G-\hat{G}||_{H_2}. |
||
| + | </math> |
||
| + | |||
| + | Initially investigated in <ref name="MeiL67"></ref>, first order necessary conditions for a local minimizer <math>\hat{G}</math> imply that its rational transfer function <math>\hat{G}(s)=\hat{c}^T (sI-\hat{A})^{-1}b</math> is a Hermite interpolant of the original transfer function at its reflected system poles, i.e., |
||
| + | |||
| + | :<math> |
||
| + | G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r, |
||
| + | </math> |
||
| + | where <math>\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\} </math> are assumed to be the single poles of <math> \hat{G} </math>. Based on the idea of rational interpolation by rational Krylov subspaces, in <ref name="GugAB08"></ref> the authors have picked up the optimality conditions and proposed to iteratively correct the projection subspaces. In pseudocode, the classical algorithm (IRKA) from <ref name="GugAB08"></ref> looks like |
||
| + | |||
| + | 1. Make an initial selection of <math>\sigma_i </math> for <math>i=1,\dots,r </math> that is closed under conjugation and fix a convergence tolerance <math>tol</math>. |
||
| + | 2. Choose <math>V_r </math> and <math> W_r</math> so that <math>\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \} </math>, <math>\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \} </math> and <math> W_r^TV_r=I</math>. |
||
| + | 3. while (relative change in <math>\{\sigma_i\} > tol</math>) |
||
| + | (a) <math>\hat{A} = W_r^TAV_r</math> |
||
| + | (b) Assign <math>\sigma_i \leftarrow -\lambda_i(\hat{A}),</math> for <math> i=1,\dots,r</math> |
||
| + | (c) Update <math>V_r</math> and <math>W_r</math> so that <math>\text{Ran}(V_r) =\{(\sigma_1 I -A)^{-1}b,\dots,(\sigma_rI-A)^{-1}b \} </math>, <math>\text{Ran}(W_r) =\{(\sigma_1 I -A^T)^{-1}c,\dots, (\sigma_rI-A^T)^{-1}c \} </math> and <math> W_r^TV_r=I</math>. |
||
| + | 4. <math>\hat{A} = W_r^TAV_r, \hat{b}= W_r^Tb, \hat{c}^T = c^TV_r.</math> |
||
| + | |||
| + | Although a rigorous convergence proof so far has only be given for symmetric state space systems <ref name="FlaBG12"></ref>, numerous experiments have shown that the algorithm often converges rapidly. |
||
| + | |||
| + | |||
| + | ==References== |
||
| + | <references> |
||
| + | |||
| + | <ref name="MeiL67"> L. Meier, D.G. Luenberger, "<span class="plainlinks">[http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1098680&tag=1 Approximation of linear constant systems]</span>", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588 1967</ref> |
||
| + | |||
| + | <ref name="GugAB08"> S. Gugercin, A.C. Antoulas, C. Beattie "<span class="plainlinks">[http://epubs.siam.org/doi/abs/10.1137/060666123 H2 Model Reduction for Large-Scale Linear Dynamical Systems]</span>", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638 2008</ref> |
||
| + | |||
| + | |||
| + | <ref name="FlaBG12"> G. Flagg, C. Beattie, S. Gugercin "<span class="plainlinks">[http://www.sciencedirect.com/science/article/pii/S0167691112000576 Convergence of the Iterative Rational Krylov Algorithm]</span>", Systems & Control Letters, vol.61, no.6, pp.688-691 2012</ref> |
||
| + | |||
| + | </ references> |
||
Revision as of 08:07, 30 May 2013
Description
The iterative rational Krylov algorithm (IRKA) is an interpolation-based model reduction method for single-input-single-output linear time systems
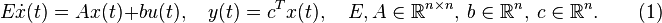 (1)
(1)
For a given system 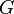 and a prescribed reduced system order
and a prescribed reduced system order  , the goal of the algorithm is to find a local minimizer
, the goal of the algorithm is to find a local minimizer 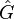 for the
for the 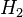 model reduction problem
model reduction problem
Initially investigated in [1], first order necessary conditions for a local minimizer 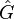 imply that its rational transfer function
imply that its rational transfer function 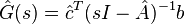 is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,
is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,
where 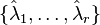 are assumed to be the single poles of
are assumed to be the single poles of 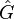 . Based on the idea of rational interpolation by rational Krylov subspaces, in [2] the authors have picked up the optimality conditions and proposed to iteratively correct the projection subspaces. In pseudocode, the classical algorithm (IRKA) from [2] looks like
. Based on the idea of rational interpolation by rational Krylov subspaces, in [2] the authors have picked up the optimality conditions and proposed to iteratively correct the projection subspaces. In pseudocode, the classical algorithm (IRKA) from [2] looks like
1. Make an initial selection offor
that is closed under conjugation and fix a convergence tolerance
. 2. Choose
and
so that
,
and
. 3. while (relative change in
) (a)
(b) Assign
for
(c) Update
and
so that
,
and
. 4.
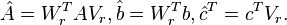
Although a rigorous convergence proof so far has only be given for symmetric state space systems [3], numerous experiments have shown that the algorithm often converges rapidly.
References
<references>
</ references>
- ↑ 1.0 1.1 L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588 1967
- ↑ 2.0 2.1 2.2 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638 2008
- ↑ 3.0 3.1 G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691 2012