Difference between revisions of "Anemometer"

Revision as of 17:17, 28 November 2011

Description

An anemometer, a flow sensing device, consists of a heater and temperature sensors before and after the heater, placed either directly in the flow or in its vicinity. They are located on a membrane to minimize heat dissipation through the structure. Without any flow, the heat dissipates symmetrically into the fluid. This symmetry is disturbed if a flow is applied to the fluid, which leads to a convection on the temperature field and therefore to a difference between the temperature sensors (see Fig.1 below) from which the fluid velocity can be determined.

The physical model can be expressed by the convection-diffusion partial differential equation[4]:

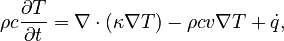
$\rho c \frac{\partial T}{\partial t} = \nabla \cdot (\kappa \nabla T ) - \rho c v \nabla T + \dot q,$

where $\rho$ denotes the mass density, $c$ is the specific heat, $\kappa$ is the thermal conductivity, $v$ is the fluid velocity, $T$ is the temperature and $\dot q$ the heat flow into the system caused by the heater.

@@ Line 18: / Line 18: @@
 <math>\rho c \frac{\partial T}{\partial t} = \nabla \cdot (\kappa
-  \nabla T ) - \rho c v \normalfont \nabla T + \dot q,</math>
+  \nabla T ) - \rho c v \nabla T + \dot q,</math>
 where <math>\rho</math> denotes the mass density, <math>c</math> is the specific heat,