Kuerschner (talk | contribs) (Created page with "Category:method Category:DAE order unspecified Category:linear Category:first differential order Category:second differential order [[Category:linear algeb...") |
Kuerschner (talk | contribs) |
||
| Line 2: | Line 2: | ||
[[Category:DAE order unspecified]] |
[[Category:DAE order unspecified]] |
||
[[Category:linear]] |
[[Category:linear]] |
||
| + | [[Category:time invariant]] |
||
[[Category:first differential order]] |
[[Category:first differential order]] |
||
[[Category:second differential order]] |
[[Category:second differential order]] |
||
| Line 10: | Line 11: | ||
<math> |
<math> |
||
| − | E |
+ | E\dot{x}(t)=A x(t)+B u(t), \quad |
y(t)=Cx(t)+Du(t) \quad \quad (1) |
y(t)=Cx(t)+Du(t) \quad \quad (1) |
||
</math> |
</math> |
||
The main idea is to construct the projection matrices as <math>V=[x_1,\ldots,x_r], W=[y_1,\ldots,y_r]</math> where the <math>x_i, y_i</math> are right and left eigenvectors corresponding to |
The main idea is to construct the projection matrices as <math>V=[x_1,\ldots,x_r], W=[y_1,\ldots,y_r]</math> where the <math>x_i, y_i</math> are right and left eigenvectors corresponding to |
||
| − | certain eigenvalues <math>\lambda_i |
+ | certain eigenvalues <math>\lambda_i\in\Lambda(A,E)</math>. The eigentriples <math>(\lambda_i,x_i,y_i)</math> satisfy. |
<math> |
<math> |
||
Ax_i=\lambda_iEx_i,\quad A^Hy_i=\overline{\lambda_i}E^Hy_i,\quad i=1,\ldots,r. |
Ax_i=\lambda_iEx_i,\quad A^Hy_i=\overline{\lambda_i}E^Hy_i,\quad i=1,\ldots,r. |
||
</math> |
</math> |
||
| + | |||
| + | They are different ways to select this typically small subset of eigenvalues. An often used criterion is to take the eigenvalue closest to the imaginary axis, i.e. the ones with the smallest real part, and their associated eigenvectors into account. Dominant pole based modal truncation selects <math>(\lambda_i,x_i,y_i)</math> with respect to their contribution in the transfer function and is described below. |
||
Revision as of 11:48, 24 April 2013
Description
Model truncation is one of the oldest MOR methods for linear time invariant systems
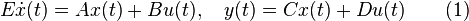
The main idea is to construct the projection matrices as ![V=[x_1,\ldots,x_r], W=[y_1,\ldots,y_r]](/morwiki/images/math/0/e/e/0ee65b7c5e9ab333049a1b288dac26d0.png) where the
where the 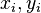 are right and left eigenvectors corresponding to
certain eigenvalues
are right and left eigenvectors corresponding to
certain eigenvalues 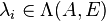 . The eigentriples
. The eigentriples 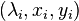 satisfy.
satisfy.
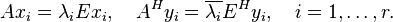
They are different ways to select this typically small subset of eigenvalues. An often used criterion is to take the eigenvalue closest to the imaginary axis, i.e. the ones with the smallest real part, and their associated eigenvectors into account. Dominant pole based modal truncation selects 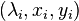 with respect to their contribution in the transfer function and is described below.
with respect to their contribution in the transfer function and is described below.
