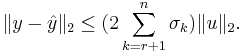m |
m |
||
| Line 4: | Line 4: | ||
| − | A stable system <math>\Sigma</math> , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations |
+ | A stable minimal (controllable and observable) system <math>\Sigma</math> , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations |
<math> AP+PA^T+BB^T=0,\quad A^TQ+QA+C^TC=0</math> |
<math> AP+PA^T+BB^T=0,\quad A^TQ+QA+C^TC=0</math> |
||
| − | satisfy <math> P=Q=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n |
+ | satisfy <math> P=Q=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n>0</math> |
The spectrum of <math> (PQ)^{\frac{1}{2}}</math> which is <math>\{\sigma_1,\dots,\sigma_n\}</math> are the Hankel singular values. |
The spectrum of <math> (PQ)^{\frac{1}{2}}</math> which is <math>\{\sigma_1,\dots,\sigma_n\}</math> are the Hankel singular values. |
||
| Line 18: | Line 18: | ||
<math> (A,B,C,D)\Rightarrow (TAT^{-1},TB,CT^{-1},D)=\left (\begin{bmatrix}A_{11} & A_{12}\\ A_{21} & A_{22}\end{bmatrix},\begin{bmatrix}B_1\\B_2\end{bmatrix}\begin{bmatrix} C_1 &C_2 \end{bmatrix},D\right)</math> |
<math> (A,B,C,D)\Rightarrow (TAT^{-1},TB,CT^{-1},D)=\left (\begin{bmatrix}A_{11} & A_{12}\\ A_{21} & A_{22}\end{bmatrix},\begin{bmatrix}B_1\\B_2\end{bmatrix}\begin{bmatrix} C_1 &C_2 \end{bmatrix},D\right)</math> |
||
| + | This transformed system has transformed Gramians <math>TPT^T</math> and <math>T^{-T}QT^{-1}</math> which are equal and diagonal. |
||
| − | |||
The truncated reduced system is then given by |
The truncated reduced system is then given by |
||
Revision as of 10:21, 27 March 2013
An important projection model reduction method which delivers high quality reduced models by making an extra effort in choosing the projection subspaces.
A stable minimal (controllable and observable) system 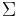 , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations
, realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations
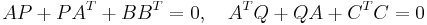
satisfy 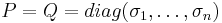 with
with 
The spectrum of 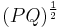 which is
which is  are the Hankel singular values.
are the Hankel singular values.
In order to do balanced truncation one has to first compute a balanced realization via state-space transformation
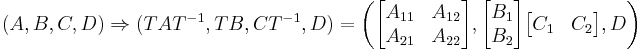 This transformed system has transformed Gramians
This transformed system has transformed Gramians 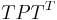 and
and 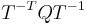 which are equal and diagonal.
The truncated reduced system is then given by
which are equal and diagonal.
The truncated reduced system is then given by
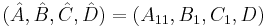
Implementation: SR Method
One computes it for example by the SR Method.
First one computes the (Cholesky) factors of the gramians 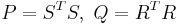 . Then we compute the singular value decomposition of
. Then we compute the singular value decomposition of 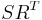
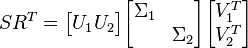
Then the reduced order model is given by 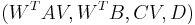 where
where
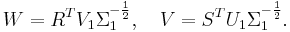
We get then that 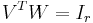 which makes
which makes 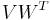 an oblique projector and hence balanced trunctation a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by
an oblique projector and hence balanced trunctation a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by  , where r is the order of the reduced system. It is possible to choose r via the computable error bound
, where r is the order of the reduced system. It is possible to choose r via the computable error bound