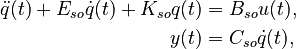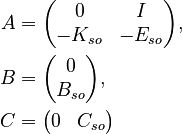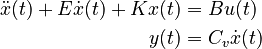(Edit SLICOT link) |
m (infobox string) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 6: | Line 6: | ||
[[Category:second differential order]] |
[[Category:second differential order]] |
||
[[Category:SISO]] |
[[Category:SISO]] |
||
| + | |||
| + | {{Infobox |
||
| + | |Title = Building Model |
||
| + | |Benchmark ID = buildingModel_n48m1q1 |
||
| + | |Category = slicot |
||
| + | |System-Class = LTI-FOS |
||
| + | |nstates = 48 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 1 |
||
| + | |nparameters = 0 |
||
| + | |components = A, B, C |
||
| + | |License = NA |
||
| + | |Creator = [[User:Himpe]] |
||
| + | |Editor = |
||
| + | * [[User:Himpe]] |
||
| + | * [[User:Mlinaric]] |
||
| + | |Zenodo-link = NA |
||
| + | }} |
||
==Description: Motion Problem in a Building== |
==Description: Motion Problem in a Building== |
||
| Line 33: | Line 51: | ||
A = mat['A'].toarray() |
A = mat['A'].toarray() |
||
B = mat['B'] |
B = mat['B'] |
||
| − | C = mat['C'].astype(np. |
+ | C = mat['C'].astype(np.float64) |
</syntaxhighlight> |
</syntaxhighlight> |
||
Latest revision as of 10:26, 30 November 2023
| Background | |
|---|---|
| Benchmark ID |
buildingModel_n48m1q1 |
| Category |
slicot |
| System-Class |
LTI-FOS |
| Parameters | |
| nstates |
48
|
| ninputs |
1 |
| noutputs |
1 |
| nparameters |
0 |
| components |
A, B, C |
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description: Motion Problem in a Building
This benchmark models the displacement of a multi-story building for example during an Earthquake. More details can be found in [1] and [2], [3].
Earthquake Model
Origin
This benchmark is part of the SLICOT Benchmark Examples for Model Reduction[3].
Data
The system matrices  ,
,  ,
,  are available from the SLICOT benchmarks page: build.zip and are stored as MATLAB .mat file.
are available from the SLICOT benchmarks page: build.zip and are stored as MATLAB .mat file.
Here is Python code for loading the matrices ( is stored as a sparse matrix that is mostly full and
is stored as a sparse matrix that is mostly full and  is stored as an array of 8-bit unsigned integers):
is stored as an array of 8-bit unsigned integers):
import numpy as np from scipy.io import loadmat mat = loadmat('build.mat') A = mat['A'].toarray() B = mat['B'] C = mat['C'].astype(np.float64)
The 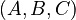 represents a second-order system
represents a second-order system
as
Here is Python code for checking the structure and extracting the second-order matrices:
n = 48 n2 = n // 2 assert np.all(A[:n2, :n2] == 0) assert np.all(A[:n2, n2:] == np.eye(n2)) assert np.all(B[:n2] == 0) assert np.all(C[:, :n2] == 0) Eso = -A[n2:, n2:] Kso = -A[n2:, :n2] Bso = B[n2:] Cso = C[:, n2:]
Dimensions
First differential order
System structure:
System dimensions:
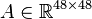 ,
,
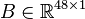 ,
,
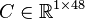 .
.
Second differential order
System structure:
System dimensions:
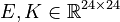 ,
,
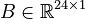 ,
,
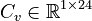 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org
@MANUAL{slicot_build,
title = {{SLICOT} - Subroutine Library in Systems and Control Theory},
organization = {Niconet e.V.}
address = {\url{http://www.slicot.org}},
key = {SLICOT}
}
- For the background on the benchmark:
@ARTICLE{morAntSG01,
author = {A.C. Antoulas, D.C. Sorensen and S. Gugercin},
title = {A survey of model reduction methods for large-scale systems},
journal = {Contemporary Mathematics},
volume = {280},
pages = {193--219},
year = {2001},
doi = {10.1090/conm/280}
}
References
- ↑ A.C. Antoulas, D.C. Sorensen and S. Gugercin. A survey of model reduction methods for large-scale systems. Contemporary Mathematics, 280: 193--219, 2001.
- ↑ Y. Chahlaoui, P. Van Dooren, A collection of Benchmark examples for model reduction of linear time invariant dynamical systems, Working Note 2002-2: 2002.
- ↑ 3.0 3.1 Y. Chahlaoui, P. Van Dooren, Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.