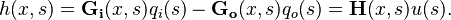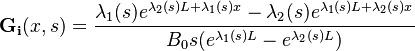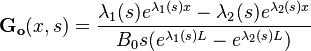m (typos) |
|||
| (20 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
| Line 8: | Line 6: | ||
===Motivation=== |
===Motivation=== |
||
| − | The so-called Saint-Venant equations are largely used in the hydraulic domain to model the dynamics of an open channel flow. These equations consist of two nonlinear hyperbolic PDEs. In the considered benchmark, under mild simplifying assumptions detailed in <ref name= Dalmas2016>V. Dalmas, G. Robert, C. Poussot-Vassal, I. Pontes-Duff and C. Seren, "From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity", in Proceedings of the European Control Conference (ECC), Aalborg, Denmark, July, 2016, pp. 1982-1987 |
+ | The so-called [[wikipedia:Shallow_water_equations|Saint-Venant equations]] are largely used in the hydraulic domain to model the dynamics of an open channel flow. These equations consist of two nonlinear hyperbolic PDEs. In the considered benchmark, under mild simplifying assumptions detailed in <ref name= Dalmas2016>V. Dalmas, G. Robert, C. Poussot-Vassal, I. Pontes-Duff and C. Seren, "<span class="plainlinks">[https://doi.org/10.1109/ECC.2016.7810582 From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity]</span>", in Proceedings of the European Control Conference (ECC), Aalborg, Denmark, July, 2016, pp. 1982-1987.</ref>, the St Venant PDE equations describing the height variation <math>h</math> of the river as a function of the inflow <math>q_i</math> and outflow <math>q_o</math> variations, at location <math>x</math> (<math>x\in[0\,\,L]</math>, <math>L\in\mathbb R_+</math>), obtained around some flow and height linearisation point, can be formulated as follows: |
:<math> |
:<math> |
||
h(x,s) = \mathbf{G_i}(x,s)q_i(s) - \mathbf{G_o}(x,s)q_o(s) = \mathbf H(x,s) u(s). |
h(x,s) = \mathbf{G_i}(x,s)q_i(s) - \mathbf{G_o}(x,s)q_o(s) = \mathbf H(x,s) u(s). |
||
</math> |
</math> |
||
| − | The <math>\mathbf G_i</math> and <math>\mathbf G_o</math> |
+ | The <math>\mathbf G_i</math> and <math>\mathbf G_o</math> are the following irrational functions: |
:<math> |
:<math> |
||
\mathbf{G_i}(x,s)= \dfrac{\lambda_1(s)e^{\lambda_2(s)L+\lambda_1(s)x}-\lambda_2(s)e^{\lambda_1(s)L+\lambda_2(s)x}}{B_0s(e^{\lambda_1(s)L}-e^{\lambda_2(s)L})} |
\mathbf{G_i}(x,s)= \dfrac{\lambda_1(s)e^{\lambda_2(s)L+\lambda_1(s)x}-\lambda_2(s)e^{\lambda_1(s)L+\lambda_2(s)x}}{B_0s(e^{\lambda_1(s)L}-e^{\lambda_2(s)L})} |
||
| Line 22: | Line 20: | ||
</math> |
</math> |
||
| − | === |
+ | ===Considered data=== |
| − | The benchmark contains the above irrational model description together with the numerical data as used in |
+ | The benchmark contains the above irrational model description together with the numerical data as used in the reference paper, given as Matlab handle functions. |
| − | + | ==Origin== |
|
| + | Collaboration between [https://www.onera.fr ONERA] and [https://www.edf.fr/ EDF]. The data from the simplified hydro-electric open-channel model come from V. Dalmas and G. Robert while and the post-processing was performed jointly by P. Vuillemin, and C. Poussot-Vassal. |
||
==Data== |
==Data== |
||
| + | ===Description=== |
||
| + | The [[File:HydroelectricChannel.zip]] (67KB) repository contains three files: |
||
| + | |||
| + | * The <tt>dataONERA_Hydroelectric.mat</tt> data file, with the data describing the irrational model described above |
||
| + | |||
| + | * The <tt>dataONERA_Hydroelectric_withMOR.mat</tt> data file, with 2 ROMs obtained with the [https://morwiki.mpi-magdeburg.mpg.de/morwiki/index.php/MORE '''MOR toolbox'''] using the Loewner method |
||
| + | ** Hr1 : linear rational ROM (state-space models in Matlab form). |
||
| + | ** Hr2 : linear rational ROM with post stability enforcement and addition of the 0 singularity afterward (state-space models in Matlab form). |
||
| + | |||
| + | * The <tt>startONERA_Hydroelectric.m</tt> script file, used to load and plot the data for illustration. |
||
| + | |||
| + | ===Objective=== |
||
| + | |||
| + | The model's main dynamics are a delayed one with an integral action. |
||
| + | Find a (linear) reduced order model stable but with one single singularity in 0 that approximates the irrational model over some frequency range (e.g. [0,0.01]rad/s) |
||
| + | |||
| + | ===Remark=== |
||
| + | As the original model is irrational and of infinite dimension, it exhibits an infinite number of singularities. Therefore, approximation over the complete frequency range is unachievable, at least with a rational function. That is why an approximation over a bounded frequency range is preferable. Indeed, strange behaviors may appear. |
||
==Citation== |
==Citation== |
||
| Line 38: | Line 55: | ||
* For the benchmark itself and its data: |
* For the benchmark itself and its data: |
||
| − | ::The MORwiki Community, '''Hydro-Electric Open Channel'''. MORwiki - Model Order Reduction Wiki, |
+ | ::The MORwiki Community, '''Hydro-Electric Open Channel'''. MORwiki - Model Order Reduction Wiki, 2021. https://morwiki.mpi-magdeburg.mpg.de/morwiki/index.php/Hydro-Electric_Open_Channel |
| + | |||
| + | * For the background on the benchmark: |
||
@inproceedings{DalmasECC:2016, |
@inproceedings{DalmasECC:2016, |
||
| − | author = {V. Dalmas and G. Robert and C. Poussot-Vassal and I. {Pontes Duff} |
+ | author = {V. Dalmas and G. Robert and C. Poussot-Vassal and I. {Pontes Duff} and C. Seren}, |
title = {From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity}, |
title = {From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity}, |
||
booktitle = {Proceedings of the 15th European Control Conference}, |
booktitle = {Proceedings of the 15th European Control Conference}, |
||
| − | address = {Aalborg, Denmark}, |
||
| − | month = {July}, |
||
year = {2016}, |
year = {2016}, |
||
| − | pages = {1982-1987}, |
+ | pages = {1982--1987}, |
| + | doi = {10.1109/ECC.2016.7810582} |
||
} |
} |
||
==References== |
==References== |
||
| + | <references /> |
||
| − | |||
==Contact== |
==Contact== |
||
| + | |||
| + | '' [[User:Poussotvassal]] '' |
||
Latest revision as of 11:11, 15 March 2022
Description
Motivation
The so-called Saint-Venant equations are largely used in the hydraulic domain to model the dynamics of an open channel flow. These equations consist of two nonlinear hyperbolic PDEs. In the considered benchmark, under mild simplifying assumptions detailed in [1], the St Venant PDE equations describing the height variation  of the river as a function of the inflow
of the river as a function of the inflow 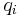 and outflow
and outflow 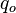 variations, at location
variations, at location  (
(![x\in[0\,\,L]](/morwiki/images/math/9/2/2/922897af4e1e015582f11b61e69808c9.png) ,
, 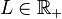 ), obtained around some flow and height linearisation point, can be formulated as follows:
), obtained around some flow and height linearisation point, can be formulated as follows:
The 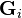 and
and 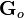 are the following irrational functions:
are the following irrational functions:
and
Considered data
The benchmark contains the above irrational model description together with the numerical data as used in the reference paper, given as Matlab handle functions.
Origin
Collaboration between ONERA and EDF. The data from the simplified hydro-electric open-channel model come from V. Dalmas and G. Robert while and the post-processing was performed jointly by P. Vuillemin, and C. Poussot-Vassal.
Data
Description
The File:HydroelectricChannel.zip (67KB) repository contains three files:
- The dataONERA_Hydroelectric.mat data file, with the data describing the irrational model described above
- The dataONERA_Hydroelectric_withMOR.mat data file, with 2 ROMs obtained with the MOR toolbox using the Loewner method
- Hr1 : linear rational ROM (state-space models in Matlab form).
- Hr2 : linear rational ROM with post stability enforcement and addition of the 0 singularity afterward (state-space models in Matlab form).
- The startONERA_Hydroelectric.m script file, used to load and plot the data for illustration.
Objective
The model's main dynamics are a delayed one with an integral action. Find a (linear) reduced order model stable but with one single singularity in 0 that approximates the irrational model over some frequency range (e.g. [0,0.01]rad/s)
Remark
As the original model is irrational and of infinite dimension, it exhibits an infinite number of singularities. Therefore, approximation over the complete frequency range is unachievable, at least with a rational function. That is why an approximation over a bounded frequency range is preferable. Indeed, strange behaviors may appear.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Hydro-Electric Open Channel. MORwiki - Model Order Reduction Wiki, 2021. https://morwiki.mpi-magdeburg.mpg.de/morwiki/index.php/Hydro-Electric_Open_Channel
- For the background on the benchmark:
@inproceedings{DalmasECC:2016,
author = {V. Dalmas and G. Robert and C. Poussot-Vassal and I. {Pontes Duff} and C. Seren},
title = {From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity},
booktitle = {Proceedings of the 15th European Control Conference},
year = {2016},
pages = {1982--1987},
doi = {10.1109/ECC.2016.7810582}
}
References
- ↑ V. Dalmas, G. Robert, C. Poussot-Vassal, I. Pontes-Duff and C. Seren, "From infinite dimensional modelling to parametric reduced order approximation: Application to open-channel flow for hydroelectricity", in Proceedings of the European Control Conference (ECC), Aalborg, Denmark, July, 2016, pp. 1982-1987.