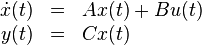m (infobox string) |
|||
| (10 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
[[Category:SLICOT]] |
[[Category:SLICOT]] |
||
| Line 7: | Line 5: | ||
[[Category:Sparse]] |
[[Category:Sparse]] |
||
| + | {{Infobox |
||
| − | '''This is a stub. Please expand.''' |
||
| + | |Title = Penzl's FOM |
||
| + | |Benchmark ID = penzlFOM_n1006m1q1 |
||
| + | |Category = slicot |
||
| + | |System-Class = LTI-FOS |
||
| + | |nstates = 1006 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 1 |
||
| + | |nparameters = 0 |
||
| + | |components = A, B, C |
||
| + | |License = NA |
||
| + | |Creator = [[User:Himpe]] |
||
| + | |Editor = |
||
| + | * [[User:Himpe]] |
||
| + | * [[User:Yue]] |
||
| + | |Zenodo-link = NA |
||
| + | }} |
||
| + | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
The benchmark system consists of the following system components: |
The benchmark system consists of the following system components: |
||
<math> |
<math> |
||
\begin{array}{rcl} |
\begin{array}{rcl} |
||
| − | A &=& \begin{pmatrix} A_1 \\ & A_2 \\ & & A_3 \\ & & & A_4 \end{pmatrix}, \ |
+ | A &=& \begin{pmatrix} A_1 \\ & A_2 \\ & & A_3 \\ & & & A_4 \end{pmatrix}, \\ |
| − | A_1 = \begin{pmatrix} -1 & 100 \\ -100 & -1 \end{pmatrix}, \; |
+ | A_1 &=& \begin{pmatrix} -1 & 100 \\ -100 & -1 \end{pmatrix}, \; |
A_2 = \begin{pmatrix} -1 & 200 \\ -200 & -1 \end{pmatrix}, \; |
A_2 = \begin{pmatrix} -1 & 200 \\ -200 & -1 \end{pmatrix}, \; |
||
A_3 = \begin{pmatrix} -1 & 400 \\ -400 & -1 \end{pmatrix}, \; |
A_3 = \begin{pmatrix} -1 & 400 \\ -400 & -1 \end{pmatrix}, \; |
||
| Line 26: | Line 41: | ||
</math> |
</math> |
||
| + | This system is a theoretical construct, but features a non-smooth [[wikipedia:Bode_plot|Bode plot]] with three spikes. |
||
===MIMO Variant=== |
===MIMO Variant=== |
||
| Line 33: | Line 49: | ||
===Parametric Variant=== |
===Parametric Variant=== |
||
| − | In, a parametric variant of this benchmark is |
+ | In <ref name="Ionita14"/>, a parametric variant of this benchmark is formulated by redefining |
<math> |
<math> |
||
A_1 = \begin{pmatrix} -1 & p \\ -p & -1 \end{pmatrix}. |
A_1 = \begin{pmatrix} -1 & p \\ -p & -1 \end{pmatrix}. |
||
| Line 99: | Line 115: | ||
<ref name="penzl06"> T. Penzl. <span class="plainlinks">[https://doi.org/10.1016/j.laa.2006.01.007 Algorithms for Model Reduction of Large Dynamical Systems]</span>. Linear Algebra and its Application 415(2--3): 322--343, 2006.</ref> |
<ref name="penzl06"> T. Penzl. <span class="plainlinks">[https://doi.org/10.1016/j.laa.2006.01.007 Algorithms for Model Reduction of Large Dynamical Systems]</span>. Linear Algebra and its Application 415(2--3): 322--343, 2006.</ref> |
||
| − | <ref name="heyouni08"> M. Heyouni, K. Jbilou, A. Messaoudi, K. Tabaa. <span class="plainlinks">[https:// |
+ | <ref name="heyouni08"> M. Heyouni, K. Jbilou, A. Messaoudi, K. Tabaa. <span class="plainlinks">[https://www.scielo.br/j/cam/a/Sq6GFZqcXSwNQKk3SmpB46p/?lang=en Model Reduction in Large-Scale MIMO Dynamical Systems via the Block Lanczos Method]</span>. Computational & Applied Mathematics 27(11): 211--236, 2008.</ref> |
<ref name="chahlaoui02"> Y. Chahlaoui, P. Van Dooren, <span class="plainlinks">[http://eprints.maths.manchester.ac.uk/1040/1/ChahlaouiV02a.pdf A collection of Benchmark examples for model reduction of linear time invariant dynamical systems]</span>, Working Note 2002-2: 2002.</ref> |
<ref name="chahlaoui02"> Y. Chahlaoui, P. Van Dooren, <span class="plainlinks">[http://eprints.maths.manchester.ac.uk/1040/1/ChahlaouiV02a.pdf A collection of Benchmark examples for model reduction of linear time invariant dynamical systems]</span>, Working Note 2002-2: 2002.</ref> |
||
<ref name="chahlaoui05"> Y. Chahlaoui, P. Van Dooren, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_24 Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems]</span>, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.</ref> |
<ref name="chahlaoui05"> Y. Chahlaoui, P. Van Dooren, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_24 Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems]</span>, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.</ref> |
||
| + | |||
| + | |||
| + | <ref name="Ionita14"> A. C. Ionita,A. C. Antoulas, <span class="plainlinks">[https://doi.org/10.1137/130914619 Data-Driven Parametrized Model Reduction in the Loewner Framework]</span>, SIAM J. Sci. Comput. 36(3): A984–A1007, 2014.</ref> |
||
</references> |
</references> |
||
Latest revision as of 10:38, 30 November 2023
| Background | |
|---|---|
| Benchmark ID |
penzlFOM_n1006m1q1 |
| Category |
slicot |
| System-Class |
LTI-FOS |
| Parameters | |
| nstates |
1006
|
| ninputs |
1 |
| noutputs |
1 |
| nparameters |
0 |
| components |
A, B, C |
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description
This benchmark is an artificial example system of order 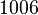 from [1] also listed in [2]. It has long been regarded as a standard "full order model" (FOM) for testing new methods.
from [1] also listed in [2]. It has long been regarded as a standard "full order model" (FOM) for testing new methods.
The benchmark system consists of the following system components:
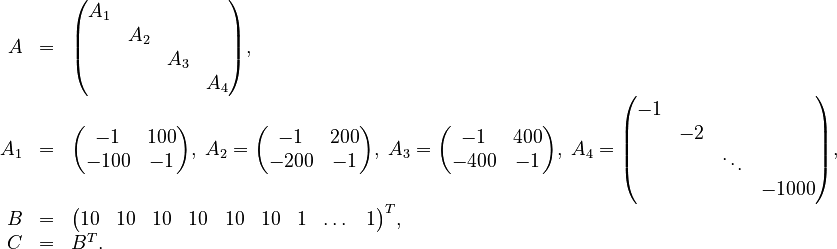
This system is a theoretical construct, but features a non-smooth Bode plot with three spikes.
MIMO Variant
In [3] a MIMO variant of this benchmark is utilized by adding random vectors to  and
and  .
.
Parametric Variant
In [4], a parametric variant of this benchmark is formulated by redefining
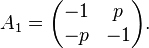
Origin
This benchmark is part of the SLICOT Benchmark Examples for Model Reduction[5].
Data
The system matrices  ,
,  ,
,  are available from the SLICOT benchmarks page: fom.zip and are stored as MATLAB .mat file.
are available from the SLICOT benchmarks page: fom.zip and are stored as MATLAB .mat file.
Dimensions
System structure:
System dimensions:
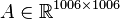 ,
,
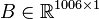 ,
,
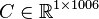 ,
,
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org
@MANUAL{slicot_fom,
title = {{SLICOT} - Subroutine Library in Systems and Control Theory},
organization = {Niconet e.V.}
address = {\url{http://www.slicot.org}},
key = {SLICOT}
}
- For the background on the benchmark:
@ARTICLE{morPen06,
author = {T. Penzl},
title = {Algorithms for Model Reduction of Large Dynamical Systems},
journal = {Linear Algebra and its Application},
volume = {415},
number = {2--3},
pages = {322--343},
year = {2006},
doi = {10.1016/j.laa.2006.01.007}
}
References
- ↑ T. Penzl. Algorithms for Model Reduction of Large Dynamical Systems. Linear Algebra and its Application 415(2--3): 322--343, 2006.
- ↑ Y. Chahlaoui, P. Van Dooren, A collection of Benchmark examples for model reduction of linear time invariant dynamical systems, Working Note 2002-2: 2002.
- ↑ M. Heyouni, K. Jbilou, A. Messaoudi, K. Tabaa. Model Reduction in Large-Scale MIMO Dynamical Systems via the Block Lanczos Method. Computational & Applied Mathematics 27(11): 211--236, 2008.
- ↑ A. C. Ionita,A. C. Antoulas, Data-Driven Parametrized Model Reduction in the Loewner Framework, SIAM J. Sci. Comput. 36(3): A984–A1007, 2014.
- ↑ Y. Chahlaoui, P. Van Dooren, Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.