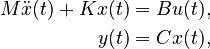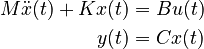m (infobox string) |
|||
| (17 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
| − | |||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
| + | [[Category:Oberwolfach]] |
||
| + | [[Category:linear]] |
||
| + | [[Category:time invariant]] |
||
| + | [[Category:second differential order]] |
||
| + | {{Infobox |
||
| − | |||
| + | |Title = Bone Model |
||
| + | |Benchmark ID = |
||
| + | * boneModelB010 |
||
| + | * boneModelB025 |
||
| + | * boneModelB050 |
||
| + | * boneModelB120 |
||
| + | * boneModelBS01 |
||
| + | * boneModelBS10 |
||
| + | |Category = oberwolfach |
||
| + | |System-Class = LTI-SOS |
||
| + | |nstates = |
||
| + | * 986703 |
||
| + | * 2159661 |
||
| + | * 4934244 |
||
| + | * 11969688 |
||
| + | * 127224 |
||
| + | * 914898 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 3 |
||
| + | |nparameters = 0 |
||
| + | |components = B, C, K, M |
||
| + | |License = GPLv2 |
||
| + | |Creator = [[User:Himpe]] |
||
| + | |Editor = |
||
| + | * [[User:Himpe]] |
||
| + | * [[User:Lund]] |
||
| + | |Zenodo-link = NA |
||
| + | }} |
||
==Description: Trabecular Bone Micro-Finite Element Models== |
==Description: Trabecular Bone Micro-Finite Element Models== |
||
| Line 12: | Line 40: | ||
<figure id="fig2">[[File:Bone2.jpg|490px|thumb|right|Figure 2]]</figure> |
<figure id="fig2">[[File:Bone2.jpg|490px|thumb|right|Figure 2]]</figure> |
||
| − | Three-dimensional serial reconstruction techniques allow us to develop very detailed micro-finite element (micro-FE) model of bones that can very accurately represent the porous bone micro-architecture. |
+ | Three-dimensional serial reconstruction techniques allow us to develop a very detailed micro-finite element (micro-FE) model of bones that can very accurately represent the porous bone micro-architecture. |
| − | + | Fig. 1 sketches the micro finite element analysis <ref name="rietbergen1995"/>. |
|
Micro [[wikipedia:CT_scan|computed tomography]] (CT) is employed to make 3D high-resolution images (~50 microns) of a bone. |
Micro [[wikipedia:CT_scan|computed tomography]] (CT) is employed to make 3D high-resolution images (~50 microns) of a bone. |
||
Then the 3D reconstruction is directly transformed into an equally shaped micro finite element model by simply converting all bone [[wikipedia:Voxel|voxels]] to equally sized 8-node brick elements. |
Then the 3D reconstruction is directly transformed into an equally shaped micro finite element model by simply converting all bone [[wikipedia:Voxel|voxels]] to equally sized 8-node brick elements. |
||
This results in [[wikipedia:Finite_Element_Method|finite element]] (FE) models with a very large number of elements. |
This results in [[wikipedia:Finite_Element_Method|finite element]] (FE) models with a very large number of elements. |
||
| − | Such models can be used, for example to study differences in bone tissue loading between healthy and [[wikipedia:Osteoporosis|osteoporotic]] human bones during quasi |
+ | Such models can be used, for example, to study differences in bone tissue loading between healthy and [[wikipedia:Osteoporosis|osteoporotic]] human bones during quasi-static loading <ref name="rietbergen2003"/>. |
There is increasing evidence, however, that bone responds in particular to dynamic loads <ref name="lanyon1984"/>. |
There is increasing evidence, however, that bone responds in particular to dynamic loads <ref name="lanyon1984"/>. |
||
| − | It has been shown that the application of high-frequency, very low |
+ | It has been shown that the application of high-frequency, very low-magnitude strains to a bone can prevent bone loss due to osteoporosis and can even result in increased bone strength in bones that are already osteoporotic. |
In order to better understand this phenomenon, it is necessary to determine the strain as sensed by the bone cells due to this loading. |
In order to better understand this phenomenon, it is necessary to determine the strain as sensed by the bone cells due to this loading. |
||
| − | This would be possible with the micro-FE analysis, but |
+ | This would be possible with the micro-FE analysis, but such an analysis needs to be a dynamic one. |
| − | The present benchmark presents six bone models varying in dimension from about two |
+ | The present benchmark presents six bone models varying in dimension from about two hundred thousand to twelve million equations with the goal to research on scalability of model reduction software. |
| − | Each model |
+ | Each model represents a second-order system of the form |
:<math> |
:<math> |
||
| − | \begin{ |
+ | \begin{align} |
| − | M \ddot{x}(t) + K x(t) &= |
+ | M \ddot{x}(t) + K x(t) &= B u(t), \\ |
| − | y(t) &= |
+ | y(t) &= C x(t), |
| − | \end{ |
+ | \end{align} |
</math> |
</math> |
||
| Line 91: | Line 119: | ||
|- |
|- |
||
|File |
|File |
||
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/BoneModel-dim1e6-BS01.dat.gz BoneModel-dim1e6-BS01.dat.gz] (305.1 kB) |
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/BoneModel-dim1e7-BS10.dat.gz BoneModel-dim1e7-BS10.dat.gz] (2.8 MB) |
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/BoneModel-dim1e7-B010.dat.gz BoneModel-dim1e7-B010.dat.gz] (3.9 MB) |
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/BoneModel-dim1e7-B025.dat.gz BoneModel-dim1e7-B025.dat.gz] (8.6 MB) |
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/BoneModel-dim1e7-B050.dat.gz BoneModel-dim1e7-B050.dat.gz] (19.6 MB) |
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/BoneModel-dim1e8-B120.dat.gz BoneModel-dim1e8-B120.dat.gz] (48.5 MB) |
|} |
|} |
||
| Line 103: | Line 131: | ||
This can be seen by comparing models <tt>BS10</tt> and <tt>B010</tt>. |
This can be seen by comparing models <tt>BS10</tt> and <tt>B010</tt>. |
||
Although models look similar by number of nonzeros in the system matrices, the model <tt>B010</tt> is much harder to solve: |
Although models look similar by number of nonzeros in the system matrices, the model <tt>B010</tt> is much harder to solve: |
||
| − | + | The number of nonzero elements in the factor for model <tt>B010</tt> is about four times more than for <tt>BS10</tt>. |
|
The method allows for the compact representation of the models, as the element mass and stiffness matrices are the same for all elements. |
The method allows for the compact representation of the models, as the element mass and stiffness matrices are the same for all elements. |
||
| Line 119: | Line 147: | ||
==Data== |
==Data== |
||
| − | The data file for each model contains the number of elements, <tt>nel</tt>, and the number of nodes, <tt>nnod</tt>, in the first line and then <tt>nel</tt> lines with eight numbers for node indices in each line. |
+ | The data file for each model contains the number of elements, <tt>nel</tt>, and the number of nodes, <tt>nnod</tt>, in the first line and then <tt>nel</tt> number of lines with eight numbers for node indices in each line. |
1) Read the element stiffness matrix elemK(24,24), 8 nodes * 3 degrees of freedom per node. |
1) Read the element stiffness matrix elemK(24,24), 8 nodes * 3 degrees of freedom per node. |
||
| Line 136: | Line 164: | ||
Do (j = 1, 24) |
Do (j = 1, 24) |
||
If (dofindex(i) < ndof AND dofindex(j) < ndof) |
If (dofindex(i) < ndof AND dofindex(j) < ndof) |
||
| − | matK(dofindex(i), dofindex(j)) += elemK(i, j) |
+ | matK(dofindex(i), dofindex(j)) += elemK(i, j) |
The input matrix contains a single column with <math>B(1) = 1</math>. |
The input matrix contains a single column with <math>B(1) = 1</math>. |
||
| − | The output matrix takes first three components of the state vector, that is, three displacements <math>UX</math>, <math>UY</math> and <math>UZ</math> for the first node. |
+ | The output matrix takes the first three components of the state vector, that is, three displacements <math>UX</math>, <math>UY</math>, and <math>UZ</math> for the first node. |
| − | The archive [https:// |
+ | The archive [https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/BoneModel-assemble.tar.gz BoneModel-assemble.tar.gz] contains the element mass and stiffness matrices as well as the sample code in [[wikipedia:C++|C++]] to assemble the dynamic system. |
The code can write the dynamic system in the [http://math.nist.gov/MatrixMarket/ Matrix Market] format or can be used as a hook to transform the global matrices to an appropriate format. |
The code can write the dynamic system in the [http://math.nist.gov/MatrixMarket/ Matrix Market] format or can be used as a hook to transform the global matrices to an appropriate format. |
||
The gzipped compressed data files for element assembly as described above can be downloaded from Table 1. |
The gzipped compressed data files for element assembly as described above can be downloaded from Table 1. |
||
Model reduction for models <tt>BS010</tt> and <tt>BS10</tt> was performed in <ref name="rudnyi2005"/>. The benchmarking of the parallel [http://graal.ens-lyon.fr/MUMPS/ MUMPS] direct solver <ref name="amestoy2006"/> for the stiffness matrices is described in <ref name="rudnyi2006"/>. |
Model reduction for models <tt>BS010</tt> and <tt>BS10</tt> was performed in <ref name="rudnyi2005"/>. The benchmarking of the parallel [http://graal.ens-lyon.fr/MUMPS/ MUMPS] direct solver <ref name="amestoy2006"/> for the stiffness matrices is described in <ref name="rudnyi2006"/>. |
||
| + | |||
| + | Files (in .mat format) can be found for the three smaller systems ([https://sparse.tamu.edu/Oberwolfach/boneS01 BS01], [https://sparse.tamu.edu/Oberwolfach/boneS10 BS10], and [https://sparse.tamu.edu/Oberwolfach/bone010 B010]) on SuiteSparse. |
||
==Dimensions== |
==Dimensions== |
||
| Line 152: | Line 182: | ||
:<math> |
:<math> |
||
| − | \begin{ |
+ | \begin{align} |
| − | M \ddot{x}(t) + K x(t) &= |
+ | M \ddot{x}(t) + K x(t) &= B u(t) \\ |
| − | y(t) &= |
+ | y(t) &= C x(t) |
| − | \end{ |
+ | \end{align} |
</math> |
</math> |
||
System dimensions: |
System dimensions: |
||
| − | <math>M \in \mathbb{R}^{ |
+ | <math>M, K \in \mathbb{R}^{n \times n}</math>, |
| − | <math> |
+ | <math>B \in \mathbb{R}^{n \times 1}</math>, |
| − | <math> |
+ | <math>C \in \mathbb{R}^{3 \times n}</math>. |
| − | <math>C \in \mathbb{R}^{3 \times N}</math>. |
||
System variants: |
System variants: |
||
| − | <tt>BS01</tt>: <math> |
+ | <tt>BS01</tt>: <math>n = 127224</math>, |
| − | <tt>BS10</tt>: <math> |
+ | <tt>BS10</tt>: <math>n = 914898</math>, |
| − | <tt>B010</tt>: <math> |
+ | <tt>B010</tt>: <math>n = 986703</math>, |
| − | <tt>B025</tt>: <math> |
+ | <tt>B025</tt>: <math>n = 2159661</math>, |
| − | <tt>B050</tt>: <math> |
+ | <tt>B050</tt>: <math>n = 4934244</math>, |
| − | <tt>B120</tt>: <math> |
+ | <tt>B120</tt>: <math>n = 11969688</math>. |
| + | |||
| + | ==Citation== |
||
| + | |||
| + | To cite this benchmark, use the following references: |
||
| + | |||
| + | * For the benchmark itself and its data: |
||
| + | ::The MORwiki Community, '''Bone Model'''. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Bone_Model |
||
| + | |||
| + | @MISC{morwiki_bone, |
||
| + | author = <nowiki>{{The MORwiki Community}}</nowiki>, |
||
| + | title = {Bone Model}, |
||
| + | howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
||
| + | url = <nowiki>{http://modelreduction.org/index.php/Bone_Model}</nowiki>, |
||
| + | year = {20XX} |
||
| + | } |
||
| + | |||
| + | * For the background on the benchmark: |
||
| + | |||
| + | @ARTICLE{RieWHetal95, |
||
| + | author = <nowiki>{B. van Rietbergen and H. Weinans and R. Huiskes and A. Odgaard}</nowiki>, |
||
| + | title = {A new method to determine trabecular bone elastic properties and loading using micromechanical finite-elements models}, |
||
| + | journal = {Journal of Biomechanics}, |
||
| + | volume = {28}, |
||
| + | number = {1}, |
||
| + | pages = {69--81}, |
||
| + | year = {1995}, |
||
| + | doi = {10.1016/0021-9290(95)80008-5} |
||
| + | } |
||
==References== |
==References== |
||
Latest revision as of 10:25, 30 November 2023
| Background | |
|---|---|
| Benchmark ID |
|
| Category |
oberwolfach |
| System-Class |
LTI-SOS |
| Parameters | |
| nstates |
|
| ninputs |
1 |
| noutputs |
3 |
| nparameters |
0 |
| components |
B, C, K, M |
| Copyright | |
| License |
GPLv2 |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description: Trabecular Bone Micro-Finite Element Models
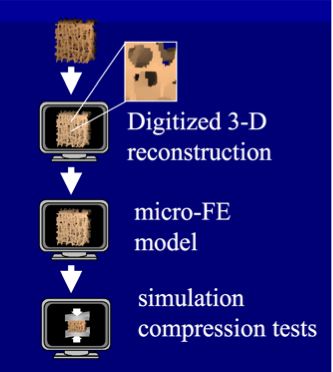
Three-dimensional serial reconstruction techniques allow us to develop a very detailed micro-finite element (micro-FE) model of bones that can very accurately represent the porous bone micro-architecture. Fig. 1 sketches the micro finite element analysis [1]. Micro computed tomography (CT) is employed to make 3D high-resolution images (~50 microns) of a bone. Then the 3D reconstruction is directly transformed into an equally shaped micro finite element model by simply converting all bone voxels to equally sized 8-node brick elements. This results in finite element (FE) models with a very large number of elements. Such models can be used, for example, to study differences in bone tissue loading between healthy and osteoporotic human bones during quasi-static loading [2].
There is increasing evidence, however, that bone responds in particular to dynamic loads [3]. It has been shown that the application of high-frequency, very low-magnitude strains to a bone can prevent bone loss due to osteoporosis and can even result in increased bone strength in bones that are already osteoporotic. In order to better understand this phenomenon, it is necessary to determine the strain as sensed by the bone cells due to this loading. This would be possible with the micro-FE analysis, but such an analysis needs to be a dynamic one.
The present benchmark presents six bone models varying in dimension from about two hundred thousand to twelve million equations with the goal to research on scalability of model reduction software. Each model represents a second-order system of the form
where the matrices  and
and 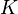 are symmetric and positive definite.
The goal of model reduction is to speed up harmonic response analysis in the frequency range
are symmetric and positive definite.
The goal of model reduction is to speed up harmonic response analysis in the frequency range 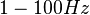 .
.
The matrix properties are given in Table 1 below.
| BS01 | BS10 | B010 | B025 | B050 | B120 | |
|---|---|---|---|---|---|---|
| Number of Elements | 20098 | 192539 | 278259 | 606253 | 1378782 | 3387547 |
| Number of Nodes | 42508 | 305066 | 329001 | 719987 | 1644848 | 3989996 |
| Number of DoFs | 127224 | 914898 | 986703 | 2159661 | 4934244 | 11969688 |
| nnz in half M | 1182804 | 9702186 | 12437739 | 27150810 | 61866069 | 151251738 |
| nnz in half K | 3421188 | 28191660 | 36326514 | 79292769 | 180663963 | 441785526 |
| File | BoneModel-dim1e6-BS01.dat.gz (305.1 kB) | BoneModel-dim1e7-BS10.dat.gz (2.8 MB) | BoneModel-dim1e7-B010.dat.gz (3.9 MB) | BoneModel-dim1e7-B025.dat.gz (8.6 MB) | BoneModel-dim1e7-B050.dat.gz (19.6 MB) | BoneModel-dim1e8-B120.dat.gz (48.5 MB) |
It should be stressed that the first two models have been obtained differently and they are much simpler to deal with than the last four. The connectivity in the last four models is about four times higher. This can be seen by comparing models BS10 and B010. Although models look similar by number of nonzeros in the system matrices, the model B010 is much harder to solve: The number of nonzero elements in the factor for model B010 is about four times more than for BS10.
The method allows for the compact representation of the models, as the element mass and stiffness matrices are the same for all elements.
As a result, a file describing the node indices for each element is enough to assemble the global matrix.
Each node has three degrees of freedom (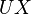 ,
, 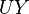 ,
, 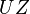 ) and it contributes three consecutive entries to the state vector.
The node numbering is natural from the first to the last.
The assembly procedure as a pseudo-code is presented below (indices start from one).
It is assumed that the last
) and it contributes three consecutive entries to the state vector.
The node numbering is natural from the first to the last.
The assembly procedure as a pseudo-code is presented below (indices start from one).
It is assumed that the last 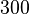 degrees of freedom are fixed as zero Dirichlet boundary conditions.
For simplicity, the pseudo-code does not take into account that the matrix is symmetric.
degrees of freedom are fixed as zero Dirichlet boundary conditions.
For simplicity, the pseudo-code does not take into account that the matrix is symmetric.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[4].
Data
The data file for each model contains the number of elements, nel, and the number of nodes, nnod, in the first line and then nel number of lines with eight numbers for node indices in each line.
1) Read the element stiffness matrix elemK(24,24), 8 nodes * 3 degrees of freedom per node.
2) Read the number of elements, nel, and number of node, nnod, from the first line of the data file.
3) Number of degrees of freedom, ndof = nnod *3 - 300.
4) Allocate space for the sparse global matrix, matK(ndof, ndof).
5) Assembly:
Do (k = 1, nel)
Read eight node numbers from the k-th line, nodeindex(8);
Construct the index for degrees of freedom, dofindex(24):
Do (i = 1, 8)
Do (j = 1, 3)
dofindex((i - 1)*3 + j)= (nodeindex(i) - 1)*3 + j;
Use dofindex to assemble the element matrix elemK:
Do (i = 1, 24)
Do (j = 1, 24)
If (dofindex(i) < ndof AND dofindex(j) < ndof)
matK(dofindex(i), dofindex(j)) += elemK(i, j)
The input matrix contains a single column with 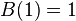 .
The output matrix takes the first three components of the state vector, that is, three displacements
.
The output matrix takes the first three components of the state vector, that is, three displacements 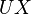 ,
, 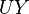 , and
, and 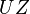 for the first node.
for the first node.
The archive BoneModel-assemble.tar.gz contains the element mass and stiffness matrices as well as the sample code in C++ to assemble the dynamic system. The code can write the dynamic system in the Matrix Market format or can be used as a hook to transform the global matrices to an appropriate format. The gzipped compressed data files for element assembly as described above can be downloaded from Table 1.
Model reduction for models BS010 and BS10 was performed in [5]. The benchmarking of the parallel MUMPS direct solver [6] for the stiffness matrices is described in [7].
Files (in .mat format) can be found for the three smaller systems (BS01, BS10, and B010) on SuiteSparse.
Dimensions
System structure:
System dimensions:
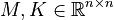 ,
,
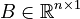 ,
,
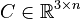 .
.
System variants:
BS01: 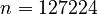 ,
BS10:
,
BS10: 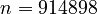 ,
B010:
,
B010: 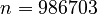 ,
B025:
,
B025: 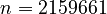 ,
B050:
,
B050: 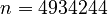 ,
B120:
,
B120: 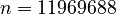 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Bone Model. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Bone_Model
@MISC{morwiki_bone,
author = {{The MORwiki Community}},
title = {Bone Model},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {http://modelreduction.org/index.php/Bone_Model},
year = {20XX}
}
- For the background on the benchmark:
@ARTICLE{RieWHetal95,
author = {B. van Rietbergen and H. Weinans and R. Huiskes and A. Odgaard},
title = {A new method to determine trabecular bone elastic properties and loading using micromechanical finite-elements models},
journal = {Journal of Biomechanics},
volume = {28},
number = {1},
pages = {69--81},
year = {1995},
doi = {10.1016/0021-9290(95)80008-5}
}
References
- ↑ B. van Rietbergen, H. Weinans, R. Huiskes, A. Odgaard, A new method to determine trabecular bone elastic properties and loading using micromechanical finite-elements models Journal of Biomechanics, 28(1): 69--81, 1995.
- ↑ B. van Rietbergen, R. Huiskes, F. Eckstein, P. Rueegsegger, Trabecular Bone Tissue Strains in the Healthy and Osteoporotic Human Femur, Journal of Bone and Mineral Research, 18(10): 1781--1787, 2003.
- ↑ L.E. Lanyon, C.T. Rubin, Static versus dynamic loads as an influence on bone remodelling, Journal of Biomechanics, 17: 897--906, 1984.
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ E.B. Rudnyi, B. van Rietbergen, J.G. Korvink. Efficient Harmonic Simulation of a Trabecular Bone Finite Element Model by means of Model Reduction. 12th Workshop "The Finite Element Method in Biomedical Engineering, Biomechanics and Related Fields", Proceedings of the 12th FEM Workshop: 61--68, 2005
- ↑ P.R. Amestoy, A. Guermouche and J.-Y. L'Excellent, S. Pralet, Hybrid scheduling for the parallel solution of linear systems. Parallel Computing, 32(2): 136--156, 2006.
- ↑ E.B. Rudnyi, B. van Rietbergen, J. G. Korvink. Model Reduction for High Dimensional Micro-FE Models. TAM'06, The Third HPC-Europa Transnational Access Meeting, Barcelona, 2006.