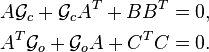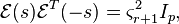| (2 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
The '''Hankel-norm approximation''' method is a model reduction approach that solves the best-approximation problem in the Hankel semi-norm<ref name="morGlo84"></ref>. |
The '''Hankel-norm approximation''' method is a model reduction approach that solves the best-approximation problem in the Hankel semi-norm<ref name="morGlo84"></ref>. |
||
| − | |||
== Description == |
== Description == |
||
Consider the standard linear-time invariant system |
Consider the standard linear-time invariant system |
||
| − | ::<math>\begin{align} \dot{x}(t) & = Ax(t) + Bu(t),\\ y(t) & = Cx(t) + Du(t), \end{align}</math> |
+ | ::<math>G:\left\{ \begin{align} \dot{x}(t) & = Ax(t) + Bu(t),\\ y(t) & = Cx(t) + Du(t), \end{align} \right.</math> |
with the matrices <math style="vertical-align: top;">A \in \mathbb{R}^{n \times n}</math>, <math style="vertical-align: top;">B \in \mathbb{R}^{n \times m}</math>, <math style="vertical-align: top;">C \in \mathbb{R}^{p \times n}</math> and <math style="vertical-align: top;">D \in \mathbb{R}^{p \times m}</math>. |
with the matrices <math style="vertical-align: top;">A \in \mathbb{R}^{n \times n}</math>, <math style="vertical-align: top;">B \in \mathbb{R}^{n \times m}</math>, <math style="vertical-align: top;">C \in \mathbb{R}^{p \times n}</math> and <math style="vertical-align: top;">D \in \mathbb{R}^{p \times m}</math>. |
||
| Line 33: | Line 32: | ||
For such error systems, the Hankel semi-norm is known to be <math>\lVert \mathcal{E} \rVert_{H} = \varsigma_{r + 1}.</math> |
For such error systems, the Hankel semi-norm is known to be <math>\lVert \mathcal{E} \rVert_{H} = \varsigma_{r + 1}.</math> |
||
| − | |||
== Algorithm == |
== Algorithm == |
||
| Line 51: | Line 49: | ||
<math>\tilde{G}(s) = \tilde{C}(sI_{n-k} - \tilde{A})^{-1}\tilde{B} + \tilde{D} = G_{r}(s) + F(s),</math> |
<math>\tilde{G}(s) = \tilde{C}(sI_{n-k} - \tilde{A})^{-1}\tilde{B} + \tilde{D} = G_{r}(s) + F(s),</math> |
||
where <math>F</math> is anti-stable and <math>G_{r}</math> is the <math>r</math>-th order stable Hankel-norm approximation. |
where <math>F</math> is anti-stable and <math>G_{r}</math> is the <math>r</math>-th order stable Hankel-norm approximation. |
||
| − | |||
== References == |
== References == |
||
Latest revision as of 10:04, 3 May 2018
The Hankel-norm approximation method is a model reduction approach that solves the best-approximation problem in the Hankel semi-norm[1].
Description
Consider the standard linear-time invariant system
with the matrices 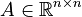 ,
, 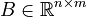 ,
, 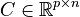 and
and 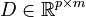 .
For a system
.
For a system 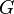 , the Hankel operator
, the Hankel operator 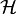 maps past inputs
maps past inputs 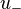 to future outputs
to future outputs 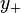 of the system, i.e.,
of the system, i.e., 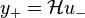 .
Then, the Hankel semi-norm of the system
.
Then, the Hankel semi-norm of the system 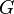 is defined as the
is defined as the 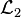 -induced norm of the Hankel opertor
-induced norm of the Hankel opertor
If the system 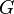 is stable, the controllability and observability Gramians
is stable, the controllability and observability Gramians 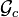 and
and 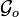 of the system above are given as the unique positive semidefinite solutions of the two Lyapunov equations
of the system above are given as the unique positive semidefinite solutions of the two Lyapunov equations
The Hankel singular values of the system 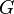 are then defined as the square-roots of the eigenvalues of the multiplied system Gramians, i.e.,
are then defined as the square-roots of the eigenvalues of the multiplied system Gramians, i.e., 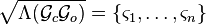 .
It can be shown, that the Hankel semi-norm of a system is given by the largest Hankel singular value
.
It can be shown, that the Hankel semi-norm of a system is given by the largest Hankel singular value 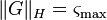 .
.
The idea of the Hankel-norm approximation method is, to construct a reduced-order model 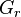 of order
of order  such that the error system
such that the error system 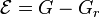 has a scaled all-pass transfer function
has a scaled all-pass transfer function
with 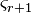 the
the 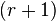 -st Hankel singular value of the system
-st Hankel singular value of the system 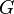 .
.
For such error systems, the Hankel semi-norm is known to be 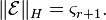
Algorithm
Here, the algorithm of the Hankel-norm approximation method is shortly described [2]:
1. Compute a minimal balanced realizationusing the balanced truncation square-root method. 2. Choose the Hankel singular value
. 3. Permute the balanced realization such that the Gramians have the form
4. Partition the resulting permuted system according to the Gramians
where
,
and
. 5. Compute the transformation
with
and
. 6. Compute the additive decomposition
where
is anti-stable and
is the
-th order stable Hankel-norm approximation.
References
- ↑ K. Glover. All optimal Hankel-norm approximations of linear multivariable systems and their
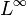 -error norms. Internat. J. Control, 39(6):1115-1193, 1984.
-error norms. Internat. J. Control, 39(6):1115-1193, 1984.
- ↑ P. Benner, E. S. Quintana-Ortí, and G. Quintana-Ortí. Computing optimal Hankel norm approximations of large-scale systems. In 2004 43rd IEEE Conference on Decision and Control (CDC), volume 3, pages 3078-3083, Atlantis, Paradise Island, Bahamas, December 2004. Institute of Electrical and Electronics Engineers.

![\lVert G \rVert_{H} := \sup\limits_{u_{-} \in \mathcal{L}_{2}\left(-\infty, 0\right]}\frac{\lVert y_{+} \rVert_{\mathcal{L}_{2}}}{\lVert u_{-} \rVert_{\mathcal{L}_{2}}}.](/morwiki/images/math/8/a/f/8af42b6ada7962159328c5a1e74e4390.png)