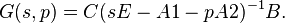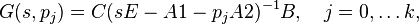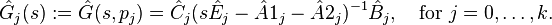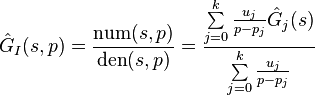| (One intermediate revision by the same user not shown) | |||
| Line 83: | Line 83: | ||
Acta Numerica, vol. 13, pp. 147-269, 2004.</ref>, <ref>M. Griebel |
Acta Numerica, vol. 13, pp. 147-269, 2004.</ref>, <ref>M. Griebel |
||
Sparse grids and related approximation schemes for higher dimensional problems |
Sparse grids and related approximation schemes for higher dimensional problems |
||
| − | In Foundations of Computational Mathematics (FoCM05), Santander |
+ | In Foundations of Computational Mathematics (FoCM05), Santander, pp. 106-161, 2006.</ref>, <ref>C. Zenger |
Sparse grids |
Sparse grids |
||
In Parallel algorithms for partial differential equations |
In Parallel algorithms for partial differential equations |
||
| − | (Kiel, 1990), vol. 31 of Notes Numer. Fluid Mech., pp. 241-251, 1991.</ref> |
+ | (Kiel, 1990), vol. 31 of Notes Numer. Fluid Mech., pp. 241-251, 1991.</ref>. |
| − | This approach is based on a hierarchical basis and a sparse tensor product |
+ | This approach is based on a hierarchical basis and a sparse tensor product construction. Significantly less interpolation points are needed for obtaining a similar accuracy as interpolation in a full grid space. |
| − | |||
| − | construction. Significantly less interpolation points are needed for obtaining a similar accuracy as interpolation in a full grid space. |
||
A coupling of [[Balanced Truncation|balanced truncation]] with piecewise polynomial interpolation using sparse grid points was described in <ref name="BauB09"/>. |
A coupling of [[Balanced Truncation|balanced truncation]] with piecewise polynomial interpolation using sparse grid points was described in <ref name="BauB09"/>. |
||
| − | |||
==Numerical results== |
==Numerical results== |
||
Latest revision as of 09:20, 17 June 2013
Transfer function interpolation is an approach for parameter-preserving model order reduction which is based on a combination of balanced truncation (or any other model order reduction method for deterministic linear, time-invariant systems) at certain distinct parameter values (the interpolation points) with interpolation. The approach is quite flexible in allowing the use of numerous interpolation techniques like polynomial, Hermite, rational, sinc, and spline interpolation.
Description
The method will exemplarily be introduced for reducing a system given by the transfer function
The PMOR approach was originally proposed in [1]
using polynomial interpolation. It can simply be extended to a hybrid approach of balanced truncation applying different kinds of interpolation.
In the following rational interpolation will be employed for the interpolation of the locally reduced-order transfer functions.
It is assumed that for 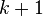 interpolation points
interpolation points 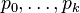 somehow distributed over the parameter interval,
the underlying non-parametric systems
somehow distributed over the parameter interval,
the underlying non-parametric systems
are stable, i.e. all finite eigenvalues of the regular pencils 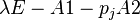 lie in the open left half of the complex plane.
lie in the open left half of the complex plane.
Then, balanced truncation can be applied to 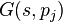 leading to reduced-order systems of order
leading to reduced-order systems of order 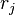
The reduced-order transfer function over the whole parameter interval is obtained by rational interpolation, e.g. by use of the barycentric formula
for real numbers 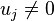 and with numerator and denominator of degree at most
and with numerator and denominator of degree at most 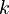 [2].
[2].
Higher dimensional parameter spaces
For systems including more than one parameter, the problem of finding a reduced-order interpolating function over the whole parameter space
is much more involved. The main reason for that is the exponentially growing number of interpolation points for higher dimensional parameter spaces.
This leads to a high computationally complexity since balanced truncation has to be applied many times. Furthermore, the order of the reduced-order
system grows exponentially as well.
A strategy for an effective and representative choice of parameter points in higher dimensional parameter spaces
comes through the use of sparse grids, see, e.g. [3], [4], [5].
This approach is based on a hierarchical basis and a sparse tensor product construction. Significantly less interpolation points are needed for obtaining a similar accuracy as interpolation in a full grid space.
A coupling of balanced truncation with piecewise polynomial interpolation using sparse grid points was described in [1].
Numerical results
Numerical results for the anemometer benchmark can be found in [6].
References
- ↑ 1.0 1.1 U. Baur and P. Benner, "Modellreduktion für parametrisierte Systeme durch balanciertes Abschneiden und Interpolation (Model Reduction for Parametric Systems Using Balanced Truncation and Interpolation)", at-Automatisierungstechnik, vol. 57, no. 8, pp. 411-420, 2009
- ↑ J.-P. Berrut, R. Baltensperger, and H.D. Mittelmann, "Recent developments in barycentric rational interpolation", in Trends and applications in constructive approximation, vol. 151 of Internat. Ser. Numer. Math., pp. 27-51. Birkhäuser, Basel, 2005.
- ↑ H.-J. Bungartz and M. Griebel, Sparse grids. Acta Numerica, vol. 13, pp. 147-269, 2004.
- ↑ M. Griebel Sparse grids and related approximation schemes for higher dimensional problems In Foundations of Computational Mathematics (FoCM05), Santander, pp. 106-161, 2006.
- ↑ C. Zenger Sparse grids In Parallel algorithms for partial differential equations (Kiel, 1990), vol. 31 of Notes Numer. Fluid Mech., pp. 241-251, 1991.
- ↑ U. Baur, P. Benner, A. Greiner, J. G. Korvink, J. Lienemann and C. Moosmann, "Parameter preserving model order reduction for MEMS applications", MCMDS Mathematical and Computer Modeling of Dynamical Systems, vol. 17, no. 4, pp. 297-317, 2011.