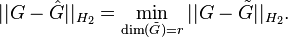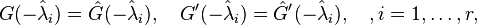m (remove link to list of abbrev) |
|||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 7: | Line 7: | ||
==Description== |
==Description== |
||
| − | + | '''IRKA''' (iterative rational Krylov algorithm) is an interpolation-based model reduction method for SISO linear time invariant systems. |
|
:<equation id="gensys" shownumber> |
:<equation id="gensys" shownumber> |
||
<math> |
<math> |
||
\dot{x}(t)=A x(t)+b u(t), \quad |
\dot{x}(t)=A x(t)+b u(t), \quad |
||
| − | y(t)=c^Tx(t),\quad |
+ | y(t)=c^Tx(t),\quad A\in\mathbb{R}^{n\times n},~b\in\mathbb{R}^{n},~c\in\mathbb{R}^{n}.\qquad (1) |
</math> |
</math> |
||
</equation> |
</equation> |
||
| Line 19: | Line 19: | ||
:<math> |
:<math> |
||
| − | ||G-\hat{G} ||_{H_2} = \min_{\text{dim}(\tilde{G})=r} ||G-\ |
+ | ||G-\hat{G} ||_{H_2} = \min_{\text{dim}(\tilde{G})=r} ||G-\tilde{G}||_{H_2}. |
</math> |
</math> |
||
| Line 27: | Line 27: | ||
G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r, |
G(-\hat{\lambda}_i) = \hat{G}(-\hat{\lambda}_i), \quad G'(-\hat{\lambda}_i) = \hat{G}'(-\hat{\lambda}_i), \quad, i =1,\dots,r, |
||
</math> |
</math> |
||
| − | where <math>\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\} </math> are assumed to be the simple poles of <math> \hat{G} </math>. Based on the idea of rational interpolation by rational Krylov subspaces, in <ref name="GugAB08"></ref> the authors have picked up the optimality conditions and proposed to iteratively correct projection subspaces until interpolation is ensured. In pseudocode, the classical |
+ | where <math>\{\hat{\lambda}_1,\dots,\hat{\lambda}_r\} </math> are assumed to be the simple poles of <math> \hat{G} </math>. Based on the idea of rational interpolation by rational Krylov subspaces, in <ref name="GugAB08"></ref> the authors have picked up the optimality conditions and proposed to iteratively correct projection subspaces until interpolation at the reflected reduced system poles is ensured. In pseudocode, the classical '''IRKA''' algorithm from <ref name="GugAB08"></ref> looks like |
1. Make an initial selection of <math>\sigma_i </math> for <math>i=1,\dots,r </math> that is closed under conjugation and fix a convergence tolerance <math>tol</math>. |
1. Make an initial selection of <math>\sigma_i </math> for <math>i=1,\dots,r </math> that is closed under conjugation and fix a convergence tolerance <math>tol</math>. |
||
| Line 37: | Line 37: | ||
4. <math>\hat{A} = W_r^TAV_r, \hat{b}= W_r^Tb, \hat{c}^T = c^TV_r.</math> |
4. <math>\hat{A} = W_r^TAV_r, \hat{b}= W_r^Tb, \hat{c}^T = c^TV_r.</math> |
||
| − | Although a rigorous convergence proof so far has only be given for symmetric state space systems <ref name="FlaBG12"></ref>, numerous experiments have shown that the algorithm often converges rapidly. |
+ | Although a rigorous convergence proof so far has only be given for symmetric state space systems <ref name="FlaBG12"></ref>, numerous experiments have shown that the algorithm often converges rapidly. Moreover, the algorithm has been extended to, e.g., multiple-input-multiple output, discrete time and differential algebraic systems. |
| + | == A minimal example == |
||
| + | |||
| + | For the lecture Model [http://www.itm.uni-stuttgart.de/courses/model_reduction/model_reduction_en.php MOR] of Mechanical System from the Institute of Engineering and Computational Mechanics University of Stuttgart a very simple example of the IRKA Algorithm were written. |
||
| + | |||
| + | The implementation with two basic exampless can be found here |
||
| + | |||
| + | [[Media:IRKA_Example.zip]] |
||
| + | |||
| + | This code is published under the BSD3-Clause License |
||
| + | All rights reserved. (c) 2015, Joerg.Fehr, University of Stuttgart |
||
==References== |
==References== |
||
<references> |
<references> |
||
| − | <ref name="MeiL67"> L. Meier, D.G. Luenberger, "<span class="plainlinks">[http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1098680&tag=1 Approximation of linear constant systems]</span>", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588 1967</ref> |
+ | <ref name="MeiL67"> L. Meier, D.G. Luenberger, "<span class="plainlinks">[http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1098680&tag=1 Approximation of linear constant systems]</span>", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588, 1967.</ref> |
| − | <ref name="GugAB08"> S. Gugercin, A.C. Antoulas, C. Beattie "<span class="plainlinks">[http://epubs.siam.org/doi/abs/10.1137/060666123 H2 Model Reduction for Large-Scale Linear Dynamical Systems]</span>", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638 2008</ref> |
+ | <ref name="GugAB08"> S. Gugercin, A.C. Antoulas, C. Beattie "<span class="plainlinks">[http://epubs.siam.org/doi/abs/10.1137/060666123 H2 Model Reduction for Large-Scale Linear Dynamical Systems]</span>", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638, 2008.</ref> |
| − | <ref name="FlaBG12"> G. Flagg, C. Beattie, S. Gugercin "<span class="plainlinks">[http://www.sciencedirect.com/science/article/pii/S0167691112000576 Convergence of the Iterative Rational Krylov Algorithm]</span>", Systems & Control Letters, vol.61, no.6, pp.688-691 2012</ref> |
+ | <ref name="FlaBG12"> G. Flagg, C. Beattie, S. Gugercin "<span class="plainlinks">[http://www.sciencedirect.com/science/article/pii/S0167691112000576 Convergence of the Iterative Rational Krylov Algorithm]</span>", Systems & Control Letters, vol.61, no.6, pp.688-691, 2012.</ref> |
| − | </ |
+ | </references> |
Latest revision as of 13:21, 11 May 2023
Description
IRKA (iterative rational Krylov algorithm) is an interpolation-based model reduction method for SISO linear time invariant systems.
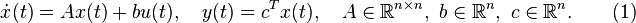 (1)
(1)
For a given system 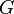 and a prescribed reduced system order
and a prescribed reduced system order  , the goal of the algorithm is to find a local minimizer
, the goal of the algorithm is to find a local minimizer 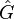 for the
for the 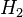 model reduction problem
model reduction problem
Initially investigated in [1], first order necessary conditions for a local minimizer 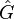 imply that its rational transfer function
imply that its rational transfer function 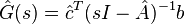 is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,
is a Hermite interpolant of the original transfer function at its reflected system poles, i.e.,
where 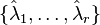 are assumed to be the simple poles of
are assumed to be the simple poles of 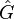 . Based on the idea of rational interpolation by rational Krylov subspaces, in [2] the authors have picked up the optimality conditions and proposed to iteratively correct projection subspaces until interpolation at the reflected reduced system poles is ensured. In pseudocode, the classical IRKA algorithm from [2] looks like
. Based on the idea of rational interpolation by rational Krylov subspaces, in [2] the authors have picked up the optimality conditions and proposed to iteratively correct projection subspaces until interpolation at the reflected reduced system poles is ensured. In pseudocode, the classical IRKA algorithm from [2] looks like
1. Make an initial selection offor
that is closed under conjugation and fix a convergence tolerance
. 2. Choose
and
so that
,
and
. 3. while (relative change in
) (a)
(b) Assign
for
(c) Update
and
so that
,
and
. 4.
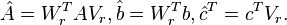
Although a rigorous convergence proof so far has only be given for symmetric state space systems [3], numerous experiments have shown that the algorithm often converges rapidly. Moreover, the algorithm has been extended to, e.g., multiple-input-multiple output, discrete time and differential algebraic systems.
A minimal example
For the lecture Model MOR of Mechanical System from the Institute of Engineering and Computational Mechanics University of Stuttgart a very simple example of the IRKA Algorithm were written.
The implementation with two basic exampless can be found here
Media:IRKA_Example.zip
This code is published under the BSD3-Clause License All rights reserved. (c) 2015, Joerg.Fehr, University of Stuttgart
References
- ↑ L. Meier, D.G. Luenberger, "Approximation of linear constant systems", IEEE Transactions on Automatic Control, vol.12, no.5, pp.585-588, 1967.
- ↑ 2.0 2.1 S. Gugercin, A.C. Antoulas, C. Beattie "H2 Model Reduction for Large-Scale Linear Dynamical Systems", SIAM. J. Matrix Anal. & Appl., vol.30, no.2, pp.609-638, 2008.
- ↑ G. Flagg, C. Beattie, S. Gugercin "Convergence of the Iterative Rational Krylov Algorithm", Systems & Control Letters, vol.61, no.6, pp.688-691, 2012.