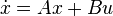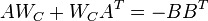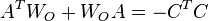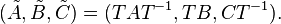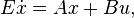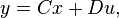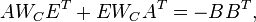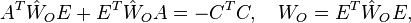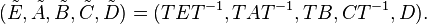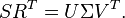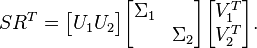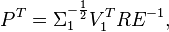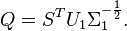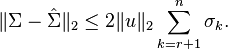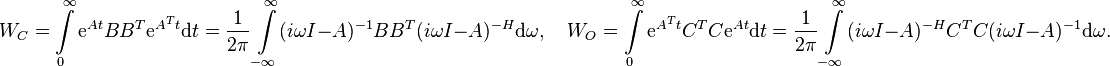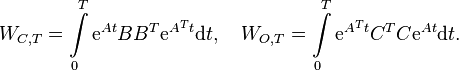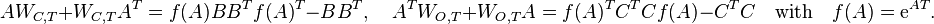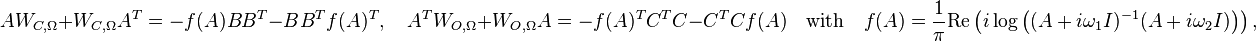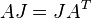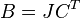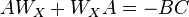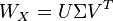m |
Kuerschner (talk | contribs) (Don't know how to cite the same paper again without increasing the counter.) |
||
| (31 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:method]] |
[[Category:method]] |
||
| + | [[Category:linear]] |
||
| + | [[Category:time invariant]] |
||
| + | [[Category:linear algebra]] |
||
| − | + | '''Balanced Truncation''' is an important [[Projection based MOR|projection]] method which delivers high quality reduced models by making an extra effort in choosing the projection subspaces based on the [[wikipedia:Controllability|Controllability]] and [[wikipedia:Observability|Observability]] of the underlying control system. |
|
| − | A stable system <math>\Sigma</math> , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations |
||
| − | <math> AP+PA^T+BB^T=0,\quad A^TQ+QA+C^TC=0</math> |
||
| + | ==Derivation == |
||
| + | A stable minimal (controllable and observable) linear system <math>\Sigma</math>, realized by <math>(A,B,C)</math> |
||
| + | :<math> \dot{x} = Ax + Bu</math> |
||
| − | satisfy <math> P=Q=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n\geq0</math> |
||
| + | :<math> y = Cx</math> |
||
| − | The spectrum of <math> (PQ)^{\frac{1}{2}}</math> which is <math>\{\sigma_1,\dots,\sigma_n\}</math> are the Hankel singular values. |
||
| + | is called balanced<ref name="moore81">B.C. Moore, "<span class="plainlinks">[http://dx.doi.org/10.1109/TAC.1981.1102568 Principal component analysis in linear systems: Controllability, observability, and model reduction]</span>", IEEE Transactions on Automatic Control , vol.26, no.1, pp.17,32, Feb 1981</ref>, if the systems [[wikipedia:Controllability_Gramian|Controllability Gramian]] and [[wikipedia:Observability_Gramian|Observability Gramian]], the solutions <math>W_C</math> and <math>W_O</math> of the Lyapunov equations |
||
| + | :<math> AW_C+W_CA^T=-BB^T </math> |
||
| − | In order to do balanced truncation one has to first compute a balanced realization via state-space transformation |
||
| + | :<math> A^TW_O+W_OA=-C^TC </math> |
||
| + | respectively, satisfy <math> W_C=W_O=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n>0</math>. |
||
| − | <math> (A,B,C,D)\Rightarrow (TAT^{-1},TB,CT^{-1},D)=\left (\begin{bmatrix}A_{11} & A_{12}\\ A_{21} & A_{22}\end{bmatrix},\begin{bmatrix}B_1\\B_2\end{bmatrix}\begin{bmatrix} C_1 &C_2 \end{bmatrix},D\right)</math> |
||
| + | Since in general, the spectrum of <math>W_CW_O</math> are the squared Hankel Singular Values for such a balanced system, they are given by: <math>\sqrt{\lambda(W_CW_O)} = \{\sigma_1,\dots,\sigma_n\}</math>. |
||
| + | An arbitrary system <math>(A,B,C)</math> can be transformed into a balanced system <math>(\tilde{A},\tilde{B},\tilde{C})</math> via a state-space transformation: |
||
| − | The truncated reduced system is then given by |
||
| − | <math> (\ |
+ | :<math> (\tilde{A},\tilde{B},\tilde{C})= (TAT^{-1},TB,CT^{-1}).</math> |
| + | This transformed system has balanced Gramians <math>W_C=T\tilde{W_C}T^T</math> and <math>W_O=T^{-T}\tilde{W_O}T^{-1}</math> which are equal and diagonal. |
||
| − | == Implementation: SR Method== |
||
| + | The balanced systems states are ordered (descendingly) by how controllable and observable they are, thus allowing a partion of the form: |
||
| − | One computes it for example by the SR Method. |
||
| − | First one computes the (Cholesky) factors of the gramians <math>P=S^TS,\; Q=R^TR</math>. Then we compute the singular value decomposition of <math> SR^T\;</math> |
||
| + | :<math> (\tilde{A},\tilde{B},\tilde{C})= \left (\begin{bmatrix}\tilde{A}_{11} & \tilde{A}_{12}\\ \tilde{A}_{21} & \tilde{A}_{22}\end{bmatrix},\begin{bmatrix}\tilde{B}_1\\\tilde{B}_2\end{bmatrix},\begin{bmatrix} \tilde{C}_1 &\tilde{C}_2 \end{bmatrix}\right)</math>. |
||
| + | By truncating the discardable states, the truncated reduced system is then given by <math> \hat{\Sigma}=(\tilde{A}_{11},\tilde{B}_1,\tilde{C}_1) </math>. |
||
| − | <math> SR^T=\begin{bmatrix} U_1 U_2 \end{bmatrix} \begin{bmatrix} \Sigma_1 & \\ & \Sigma_2\end{bmatrix} \begin{bmatrix} V_1^T\\V_2^T\end{bmatrix}</math> |
||
| + | == Generalization == |
||
| − | Then the reduced order model is given by <math>(W^TAV,W^TB,CV,D)\;</math> where |
||
| + | Considering a linear time-invariant systems, defined in generalized state-space form by |
||
| − | <math> W=R^T V_1\Sigma_1^{-\frac{1}{2}},\quad V= S^T U_1 \Sigma_1^{-\frac{1}{2}}.</math> |
||
| + | :<math> E\dot{x} = Ax + Bu,</math> |
||
| + | ::<math> y = Cx + Du,</math> |
||
| + | where nonsingularity of <math>E</math> and stability (<math>A - \lambda E</math> stable) is assumed. |
||
| − | We get then that <math>V^TW=I_r</math> which makes <math> VW^T</math> an oblique projector and hence balanced trunctation a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by <math>\sigma_1,\dots,\sigma_r</math>. It is possible to choose r via the computable error bound |
||
| + | Similarly, a stable minimal (controllable and observable) system <math>\Sigma</math>, realized by <math>(E,A,B,C,D)</math>, |
||
| − | <math> \|y-\hat{y}\|_2\leq (2\sum_{k=r+1}^n\sigma_k)\|u\|_2. </math> |
||
| + | is called balanced<ref name="moore81"/>, if the systems [[wikipedia:Controllability_Gramian|Controllability Gramian]] and [[wikipedia:Observability_Gramian|Observability Gramian]], i.e. the solutions <math>W_C</math> and <math>W_O</math> of the generalized Lyapunov equations |
||
| + | |||
| + | :<math> AW_CE^T+EW_CA^T=-BB^T, </math> |
||
| + | |||
| + | :<math> A^T\hat W_OE+E^T\hat W_OA=-C^TC, \quad W_O=E^T\hat W_O E, </math> |
||
| + | |||
| + | satisfy <math> W_C=W_O=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n>0</math>. |
||
| + | |||
| + | Again, an arbitrary system <math>(E,A,B,C,D)</math> can be transformed into a balanced system <math>(\tilde{E},\tilde{A},\tilde{B},\tilde{C},\tilde{D})</math> via a state-space transformation: |
||
| + | |||
| + | :<math> (\tilde{E},\tilde{A},\tilde{B},\tilde{C},\tilde{D})= (TET^{-1},TAT^{-1},TB,CT^{-1},D).</math> |
||
| + | |||
| + | The balanced systems states are ordered (descendingly) by how controllable and observable they are, thus allowing a partion of the form: |
||
| + | |||
| + | :<math> (\tilde{E},\tilde{A},\tilde{B},\tilde{C},\tilde{D})= \left (\begin{bmatrix}\tilde{E}_{11} & \tilde{E}_{12}\\ \tilde{E}_{21} & \tilde{E}_{22}\end{bmatrix}, \begin{bmatrix}\tilde{A}_{11} & \tilde{A}_{12}\\ \tilde{A}_{21} & \tilde{A}_{22}\end{bmatrix},\begin{bmatrix}\tilde{B}_1\\\tilde{B}_2\end{bmatrix},\begin{bmatrix} \tilde{C}_1 &\tilde{C}_2 \end{bmatrix},\tilde{D}\right)</math>. |
||
| + | |||
| + | By truncating the discardable states, the truncated reduced system is then given by <math> \hat{\Sigma}=(\tilde{E}_{11},\tilde{A}_{11},\tilde{B}_1,\tilde{C}_1,\tilde{D}) </math>. |
||
| + | |||
| + | == Balancing and Truncation == |
||
| + | |||
| + | The necessary balancing transformation can be computed by the Square-Root method<ref>A.J. Laub; M.T. Heath; C. Paige; R. Ward, "<span class="plainlinks">[http://dx.doi.org/10.1109/TAC.1987.1104549 Computation of system balancing transformations and other applications of simultaneous diagonalization algorithms]</span>," IEEE Transactions on Automatic Control, vol.32, no.2, pp.115,122, Feb 1987</ref>. |
||
| + | First, the [[wikipedia:Cholesky_decomposition|Cholesky factors]] of the Gramians <math>W_C=S^TS,\; W_O=R^TR</math> are computed. |
||
| + | Alternatively to the Cholesky factorization, the [[wikipedia:Singular_Value_Decomposition|Singular Value Decomposition]] can be employed: <math>W_O = U_O \Sigma_O U_O^T \Rightarrow S = (U_O \Sigma_O^\frac{1}{2})^T</math> and <math>W_C = U_C \Sigma_C U_C^T \Rightarrow R = (U_C \Sigma_C^\frac{1}{2})^T</math>. |
||
| + | Next, the Singular Value Decomposition of <math> SR^T\;</math> is computed: |
||
| + | |||
| + | :<math> SR^T= U\Sigma V^T.</math> |
||
| + | |||
| + | Now, partitioning <math>U,V</math>, for example based on the [[wikipedia:Hankel_singular_value|Hankel Singular Values]], gives |
||
| + | |||
| + | :<math>SR^T= \begin{bmatrix} U_1 U_2 \end{bmatrix} \begin{bmatrix} \Sigma_1 & \\ & \Sigma_2\end{bmatrix} \begin{bmatrix} V_1^T\\V_2^T\end{bmatrix}.</math> |
||
| + | |||
| + | The truncation of discardable partitions <math>U_2,V^T_2,\Sigma_2</math> results in the reduced order model <math>(P^TEQ,P^TAQ,P^TB,CQ,D)\;</math> where |
||
| + | |||
| + | :<math> P^T=\Sigma_1^{-\frac{1}{2}}V_1^T R E^{-1},</math> |
||
| + | |||
| + | :<math> Q= S^T U_1 \Sigma_1^{-\frac{1}{2}}.</math> |
||
| + | |||
| + | Note that <math>P^TEQ=I_r</math> which makes it to an oblique projector and hence '''Balanced Truncation''' a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by <math>\sigma_1,\dots,\sigma_r</math>, where r is the order of the reduced system. It is possible to choose <math>r</math> via the computable error bound<ref>D.F. Enns, "<span class="plainlinks">[http://dx.doi.org/10.1109/CDC.1984.272286 Model reduction with balanced realizations: An error bound and a frequency weighted generalization]</span>," The 23rd IEEE Conference on Decision and Control, vol.23, pp.127,132, Dec. 1984</ref>: |
||
| + | |||
| + | :<math> \|\Sigma-\hat{\Sigma}\|_2 \leq 2 \|u\|_2 \sum_{k=r+1}^n\sigma_k. </math> |
||
| + | |||
| + | == Time- and frequency-limited BT == |
||
| + | |||
| + | '''Time- and frequency-limited BT''' <ref>Gawronski, Juang "<span class="plainlinks">[http://dx.doi.org/10.1080/00207729008910366 Model reduction in limited time and frequency intervals]</span>", Int. J. Syst. Sci. 21(2), pp.349–376, 1990;</ref> are modifications of BT targeted at achieving a high approximation quality within finite time <math>[0,T], T<\infty</math> or frequency regions <math>[\omega_1,\omega_2], 0\leq\omega_1<\omega_2<\infty</math>, while allowing large approximation errors outside these regions. Starting point of the derivation are the integral expressions of the Gramians |
||
| + | |||
| + | :<math> W_{C}=\int\limits_0^{\infty}\mathrm{e}^{At}BB^T \mathrm{e}^{A^Tt}\mathrm{d}t=\frac{1}{2\pi}\int\limits_{-\infty}^{\infty}(i\omega I-A)^{-1}BB^T (i\omega I-A)^{-H}\mathrm{d}\omega,\quad W_O=\int\limits_0^{\infty}\mathrm{e}^{A^Tt}C^TC \mathrm{e}^{At}\mathrm{d}t=\frac{1}{2\pi}\int\limits_{-\infty}^{\infty}(i\omega I-A)^{-H}C^TC (i\omega I-A)^{-1}\mathrm{d}\omega.</math> |
||
| + | |||
| + | Restricting the integration domain of the time-domain integrals to <math>[0,T]</math> leads to the time-limited Gramians |
||
| + | |||
| + | :<math> W_{C,T}=\int\limits_0^{T}\mathrm{e}^{At}BB^T \mathrm{e}^{A^Tt}\mathrm{d}t,\quad W_{O,T}=\int\limits_0^{T}\mathrm{e}^{A^Tt}C^TC \mathrm{e}^{At}\mathrm{d}t.</math> |
||
| + | |||
| + | which are the solutions of the time-limited Lyapunov equations |
||
| + | |||
| + | :<math> AW_{C,T}+W_{C,T}A^T=f(A)BB^Tf(A)^T-BB^T,\quad A^TW_{O,T}+W_{O,T}A=f(A)^TC^TCf(A)-C^TC\quad\text{with}\quad f(A)= \mathrm{e}^{AT}.</math> |
||
| + | |||
| + | Likewise, restricting the frequency-domain integral expressions of <math>W_C,W_0</math> to <math>\Omega:=[-\omega_2,-\omega_2]\cup[\omega_1,\omega_2]</math> leads to the frequency-limited Lyapunov equations |
||
| + | |||
| + | :<math> AW_{C,\Omega}+W_{C,\Omega}A^T=-f(A)BB^T-BB^Tf(A)^T,\quad A^TW_{O,\Omega}+W_{O,\Omega}A=-f(A)^TC^TC-C^TCf(A)\quad\text{with}\quad f(A)= \frac{1}{\pi}\mathrm{Re}\left(i\log\left((A+i\omega_1I)^{-1}(A+i\omega_2I)\right)\right),</math> |
||
| + | |||
| + | see, e.g., <ref>Petersson, D."<span class="plainlinks">[http://www.diva-portal.org/smash/get/diva2:647068/FULLTEXT01.pdf A Nonlinear Optimization Approach to H2-Optimal Modeling and Control]</span>", PhD thesis, Linköping University, 2013.</ref>. '''Time-limited''' and '''Frequency-limited BT''' are then obtained by using Cholesky- or low-rank factors of the restricted Gramians <math>W_{C,T},W_{O,T}</math> and, respectively,<math>W_{C,\Omega},W_{O,\Omega}</math> instead of the infinite Gramians <math>W_C,W_0</math>. |
||
| + | |||
| + | Computational strategies for large-scale systems for dealing with the matrix functions <math>f(A)</math> and for computing the required low-rank factors of Gramians <math>W_{C,\Omega},W_{O,\Omega}</math> and <math>W_{C,T},W_{O,T}</math> are proposed in <ref>Benner, P., Kürschner, P., Saak, J. "<span class="plainlinks">[http://dx.doi.org/10.1137/15M1030911 Frequency-Limited Balanced Truncation with Low-Rank Approximations]</span>". SIAM J. Sci. Comp. 38(1), pp. A471-–A499, 2016.</ref>, <ref>Kürschner, P. "<span class="plainlinks">[https://arxiv.org/abs/1707.02839 Balanced truncation model order reduction in limited time intervals for large systems]</span>". arXiv e-print no. 1707.02839, 2017.</ref>. |
||
| + | |||
| + | The handling of generalized state-space systems can be adopted right away from the unrestricted BT case. |
||
| + | |||
| + | In general, neither time- nor frequency-limited BT guarantee that the stability of the original system is preserved and, hence, do also not provide an <math>H_{\infty}</math> error bound similar to the one of unrestricted BT. |
||
| + | Modified time- or frequency-limited BT <ref>Antoulas, A. C., Gugercin, S."<span class="plainlinks">[http://dx.doi.org/10.1080/00207170410001713448 A survey of model reduction by balanced truncation and some new results]</span>". Int. J. Control 77(8), pp. 748–766, 2004.</ref> fixes this, but has been found to be inferior compared to unrestricted BT and (unmodified) time-/frequency-limited BT in terms of computational efficiency. The achieved accuracy is also lower compared to time-/frequency-limited BT. |
||
| + | In <ref>Redmann, M., Kürschner, P. "<span class="plainlinks">[https://arxiv.org/abs/1710.07572 An H2-Type Error Bound for Time-Limited Balanced Truncation]</span>". arXiv e-print no. 1710.07572, 2017.</ref> H2-type error bounds for '''Time-limited BT''' are derived which do not rely on stability preservation. Moreover, some experiments in <ref>Kürschner, P. "<span class="plainlinks">[https://arxiv.org/abs/1707.02839 Balanced truncation model order reduction in limited time intervals for large systems]</span>". arXiv e-print no. 1707.02839, 2017.</ref> indicate that '''Time-limited BT''' might be a potential candidate for reducing unstable systems. |
||
| + | |||
| + | == Cross Gramian MOR == |
||
| + | |||
| + | A related Gramian-based approach is '''Cross Gramian Model Order Reduction'''<ref>Antoulas, A. C. "<span class="plainlinks">[http://dx.doi.org/10.1137/1.9780898718713 Approximation of large-scale dynamical systems]</span>". Vol. 6. Society for Industrial and Applied Mathematics, pp.376--377, 2009; ISBN 978-0-89871-529-3</ref>,<ref>D.C. Sorensen and A.C. Antoulas "<span class="plainlinks">[http://10.1016/S0024-3795(02)00283-5 The Sylvester equation and approximate balanced reduction]</span>", Linear Algebra and its Applications, vol. 351-352(0), pp. 671-700, 2002, |
||
| + | </ref>. |
||
| + | Given a stable and symmetric system <math>(A,B,C,D)</math>, such that there exists a transformation <math>J</math> |
||
| + | |||
| + | :<math>AJ = JA^T</math> |
||
| + | |||
| + | :<math>B = JC^T</math> |
||
| + | |||
| + | then the solution of the [[wikipedia:Sylvester_Equation|Sylvester Equation]] |
||
| + | |||
| + | :<math>AW_X+W_XA=-BC</math> |
||
| + | |||
| + | is the [[wikipedia:Cross_Gramian|Cross Gramian]], of which the absolute value of its spectrum equals the Hankel Singular Values: |
||
| + | |||
| + | :<math>|\lambda(W_X)| = \{\sigma_1,\dots,\sigma_r\}</math>. |
||
| + | |||
| + | Thus the [[wikipedia:Singular_Value_Decomposition|Singular Value Decomposition]] of the Cross Gramian |
||
| + | |||
| + | :<math>W_X = U\Sigma V^T</math> |
||
| + | |||
| + | also allows a partitioning |
||
| + | |||
| + | :<math>W_X = \begin{bmatrix} U_1 U_2 \end{bmatrix} \begin{bmatrix} \Sigma_1 & \\ & \Sigma_2\end{bmatrix} \begin{bmatrix} V_1^T\\V_2^T\end{bmatrix}.</math> |
||
| + | |||
| + | and a subsequent truncation of the discardable states, to which the above error bound also applies. Note that, although the similarities to the standard balanced truncation approach, the reduced order model obtained with this method is not balanced for non-symmetric systems. |
||
==References== |
==References== |
||
| + | |||
| + | <references/> |
||
Latest revision as of 17:01, 17 January 2018
Balanced Truncation is an important projection method which delivers high quality reduced models by making an extra effort in choosing the projection subspaces based on the Controllability and Observability of the underlying control system.
Derivation
A stable minimal (controllable and observable) linear system 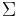 , realized by
, realized by 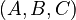
is called balanced[1], if the systems Controllability Gramian and Observability Gramian, the solutions 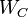 and
and 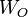 of the Lyapunov equations
of the Lyapunov equations
respectively, satisfy 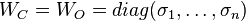 with
with  .
Since in general, the spectrum of
.
Since in general, the spectrum of 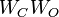 are the squared Hankel Singular Values for such a balanced system, they are given by:
are the squared Hankel Singular Values for such a balanced system, they are given by: 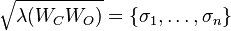 .
.
An arbitrary system 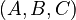 can be transformed into a balanced system
can be transformed into a balanced system 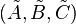 via a state-space transformation:
via a state-space transformation:
This transformed system has balanced Gramians 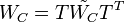 and
and 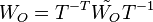 which are equal and diagonal.
The balanced systems states are ordered (descendingly) by how controllable and observable they are, thus allowing a partion of the form:
which are equal and diagonal.
The balanced systems states are ordered (descendingly) by how controllable and observable they are, thus allowing a partion of the form:
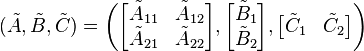 .
.
By truncating the discardable states, the truncated reduced system is then given by 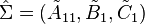 .
.
Generalization
Considering a linear time-invariant systems, defined in generalized state-space form by
where nonsingularity of  and stability (
and stability ( stable) is assumed.
stable) is assumed.
Similarly, a stable minimal (controllable and observable) system 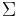 , realized by
, realized by 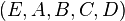 ,
is called balanced[1], if the systems Controllability Gramian and Observability Gramian, i.e. the solutions
,
is called balanced[1], if the systems Controllability Gramian and Observability Gramian, i.e. the solutions 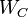 and
and 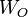 of the generalized Lyapunov equations
of the generalized Lyapunov equations
satisfy 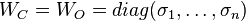 with
with  .
.
Again, an arbitrary system 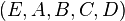 can be transformed into a balanced system
can be transformed into a balanced system 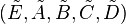 via a state-space transformation:
via a state-space transformation:
The balanced systems states are ordered (descendingly) by how controllable and observable they are, thus allowing a partion of the form:
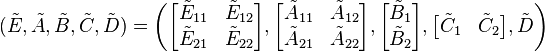 .
.
By truncating the discardable states, the truncated reduced system is then given by 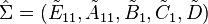 .
.
Balancing and Truncation
The necessary balancing transformation can be computed by the Square-Root method[2].
First, the Cholesky factors of the Gramians 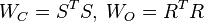 are computed.
Alternatively to the Cholesky factorization, the Singular Value Decomposition can be employed:
are computed.
Alternatively to the Cholesky factorization, the Singular Value Decomposition can be employed: 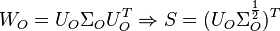 and
and 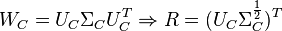 .
Next, the Singular Value Decomposition of
.
Next, the Singular Value Decomposition of 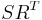 is computed:
is computed:
Now, partitioning 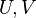 , for example based on the Hankel Singular Values, gives
, for example based on the Hankel Singular Values, gives
The truncation of discardable partitions 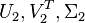 results in the reduced order model
results in the reduced order model 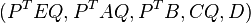 where
where
Note that 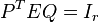 which makes it to an oblique projector and hence Balanced Truncation a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by
which makes it to an oblique projector and hence Balanced Truncation a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by  , where r is the order of the reduced system. It is possible to choose
, where r is the order of the reduced system. It is possible to choose  via the computable error bound[3]:
via the computable error bound[3]:
Time- and frequency-limited BT
Time- and frequency-limited BT [4] are modifications of BT targeted at achieving a high approximation quality within finite time ![[0,T], T<\infty](/morwiki/images/math/0/4/d/04d40c8048e99ee52a896831ade24f3a.png) or frequency regions
or frequency regions ![[\omega_1,\omega_2], 0\leq\omega_1<\omega_2<\infty](/morwiki/images/math/d/3/7/d37e7256132e8270e0fac5301206c853.png) , while allowing large approximation errors outside these regions. Starting point of the derivation are the integral expressions of the Gramians
, while allowing large approximation errors outside these regions. Starting point of the derivation are the integral expressions of the Gramians
Restricting the integration domain of the time-domain integrals to ![[0,T]](/morwiki/images/math/b/7/4/b74093923941d33ee19becc5f4b48b25.png) leads to the time-limited Gramians
leads to the time-limited Gramians
which are the solutions of the time-limited Lyapunov equations
Likewise, restricting the frequency-domain integral expressions of 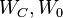 to
to ![\Omega:=[-\omega_2,-\omega_2]\cup[\omega_1,\omega_2]](/morwiki/images/math/f/b/3/fb3180d32bbfc5c43234d4db1da9b5a6.png) leads to the frequency-limited Lyapunov equations
leads to the frequency-limited Lyapunov equations
see, e.g., [5]. Time-limited and Frequency-limited BT are then obtained by using Cholesky- or low-rank factors of the restricted Gramians 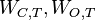 and, respectively,
and, respectively,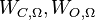 instead of the infinite Gramians
instead of the infinite Gramians 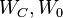 .
.
Computational strategies for large-scale systems for dealing with the matrix functions 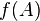 and for computing the required low-rank factors of Gramians
and for computing the required low-rank factors of Gramians 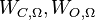 and
and 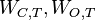 are proposed in [6], [7].
are proposed in [6], [7].
The handling of generalized state-space systems can be adopted right away from the unrestricted BT case.
In general, neither time- nor frequency-limited BT guarantee that the stability of the original system is preserved and, hence, do also not provide an 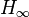 error bound similar to the one of unrestricted BT.
Modified time- or frequency-limited BT [8] fixes this, but has been found to be inferior compared to unrestricted BT and (unmodified) time-/frequency-limited BT in terms of computational efficiency. The achieved accuracy is also lower compared to time-/frequency-limited BT.
In [9] H2-type error bounds for Time-limited BT are derived which do not rely on stability preservation. Moreover, some experiments in [10] indicate that Time-limited BT might be a potential candidate for reducing unstable systems.
error bound similar to the one of unrestricted BT.
Modified time- or frequency-limited BT [8] fixes this, but has been found to be inferior compared to unrestricted BT and (unmodified) time-/frequency-limited BT in terms of computational efficiency. The achieved accuracy is also lower compared to time-/frequency-limited BT.
In [9] H2-type error bounds for Time-limited BT are derived which do not rely on stability preservation. Moreover, some experiments in [10] indicate that Time-limited BT might be a potential candidate for reducing unstable systems.
Cross Gramian MOR
A related Gramian-based approach is Cross Gramian Model Order Reduction[11],[12].
Given a stable and symmetric system 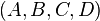 , such that there exists a transformation
, such that there exists a transformation 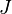
then the solution of the Sylvester Equation
is the Cross Gramian, of which the absolute value of its spectrum equals the Hankel Singular Values:
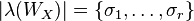 .
.
Thus the Singular Value Decomposition of the Cross Gramian
also allows a partitioning
and a subsequent truncation of the discardable states, to which the above error bound also applies. Note that, although the similarities to the standard balanced truncation approach, the reduced order model obtained with this method is not balanced for non-symmetric systems.
References
- ↑ 1.0 1.1 B.C. Moore, "Principal component analysis in linear systems: Controllability, observability, and model reduction", IEEE Transactions on Automatic Control , vol.26, no.1, pp.17,32, Feb 1981
- ↑ A.J. Laub; M.T. Heath; C. Paige; R. Ward, "Computation of system balancing transformations and other applications of simultaneous diagonalization algorithms," IEEE Transactions on Automatic Control, vol.32, no.2, pp.115,122, Feb 1987
- ↑ D.F. Enns, "Model reduction with balanced realizations: An error bound and a frequency weighted generalization," The 23rd IEEE Conference on Decision and Control, vol.23, pp.127,132, Dec. 1984
- ↑ Gawronski, Juang "Model reduction in limited time and frequency intervals", Int. J. Syst. Sci. 21(2), pp.349–376, 1990;
- ↑ Petersson, D."A Nonlinear Optimization Approach to H2-Optimal Modeling and Control", PhD thesis, Linköping University, 2013.
- ↑ Benner, P., Kürschner, P., Saak, J. "Frequency-Limited Balanced Truncation with Low-Rank Approximations". SIAM J. Sci. Comp. 38(1), pp. A471-–A499, 2016.
- ↑ Kürschner, P. "Balanced truncation model order reduction in limited time intervals for large systems". arXiv e-print no. 1707.02839, 2017.
- ↑ Antoulas, A. C., Gugercin, S."A survey of model reduction by balanced truncation and some new results". Int. J. Control 77(8), pp. 748–766, 2004.
- ↑ Redmann, M., Kürschner, P. "An H2-Type Error Bound for Time-Limited Balanced Truncation". arXiv e-print no. 1710.07572, 2017.
- ↑ Kürschner, P. "Balanced truncation model order reduction in limited time intervals for large systems". arXiv e-print no. 1707.02839, 2017.
- ↑ Antoulas, A. C. "Approximation of large-scale dynamical systems". Vol. 6. Society for Industrial and Applied Mathematics, pp.376--377, 2009; ISBN 978-0-89871-529-3
- ↑ D.C. Sorensen and A.C. Antoulas "The Sylvester equation and approximate balanced reduction", Linear Algebra and its Applications, vol. 351-352(0), pp. 671-700, 2002,