Moment-matching method

The moment-matching methods are also called the Krylov subspace methods, as well as 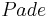$Pade$ approximation methods. These methods are applicable for non-parametric linear time invariant systems, often the descriptor systems, e.g.

$E \frac{dx(t)}{dt}=A x(t)+B u(t), \quad y(t)=Cx(t), \quad \quad (1)$

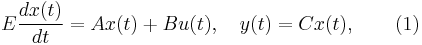
They are very efficient in many engineering applications, circuit simulation, Microelectromechanical systems(MEMS) simulation, etc..

The basic steps are as follows. First, the transfer function

$H(s)=Y(s)/U(s)=C(sE-A)^{-1}B$

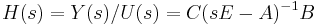
is expanded into a power series at an expansion point 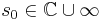$s_0\in\mathbb{C}\cup \infty$.

Let 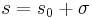$s=s_0+\sigma$, then, within the convergence radius of the series, we have

$H(s_0 + \sigma)= L^T[(s_{0}+\sigma){I}-A]^{-1}B$

$=L^T[\sigma { I}+(s_{0}{ I}-{ A})]^{-1}B$

$=L^T[{ I}-\sigma(s_0{ I}-{ A})^{-1}]^{-1}[-(s_0{ I}-{ A})]^{-1}B$

$=L^T[{ I}+\sigma(s_0{ I}- A )^{-1}+\sigma^2[(s_0{ I}-{ A})^{-1}]^{2}+\ldots]\times \quad({ A}-s_0{I})^{-1}B$

$=\sum \limits^\infty_{i=0}\underbrace{L^T[(s_0{ I}-{A})^{-1}]^i({ A}-s_0{ I})^{-1}B}_{:= m_i(s_0)} \, \sigma^i,$

where $m_i(s_0)$ are called the moments of the transfer function about $s_0$ for $i=0,1,2,\ldots$. If the expansion point is chosen as zero then the moments simplify to $m_i(0)=L^\mathrm{T}(-A^{-1})^{i+1}B$. For $s_0=\infty$ the moments are also called Markov parameters which can be computed by $L^\mathrm{T} \bA^{i-1}B$.

The goal in moment-matching model reduction is the construction of a reduced order system where some moments $\hat m_i$ of the associated transfer function $\hat H$ match some moments of the original transfer function $H$. A few important classes of approximations are listed in Table~\ref{tab:moments}. % % \begin{center} \begin{table*}[ht] \hfill{} \begin{tabular}{l|ll} %\hline Name of reduced order system& Matched moments &\\\hline %\cline{3-4} %\hline Pad\'e approximation~\cite{Bak75} & $m_i(s_0) = \hat m_i(s_0)$, & $i=0,1,\cdots,2r-1$ \\ Partial realization~\cite{GraL83} & $m_i(\infty) = \hat m_i(\infty)$, & $i=0,1,\cdots,2r-1$ \\ Multipoint Pad\'e approximation or & $m_i(s_j) = \hat m_i(s_j)$, & $i=0,1,\cdots,2r_j-1$, for $j=1,\cdots,k$, and $r_1+\dots+r_k = r$ \\ rational interpolation~\cite{AndA90,Bak75} & & %\hline \end{tabular} \hfill{} \caption{Some examples for model reduction by moment-matching.} \label{tab:moments} \end{table*} \end{center}