| Line 7: | Line 7: | ||
We use the system |
We use the system |
||
<math> |
<math> |
||
| − | E \frac{d{\bf x}}{dt}=A {\bf x}+B {\bf u}(t), |
+ | E \frac{d{\bf x}}{dt}=A {\bf x}+B {\bf u}(t),</math> |
| + | <math> |
||
{\bf y}(t)=C{\bf x}+D{\bf u}(t). |
{\bf y}(t)=C{\bf x}+D{\bf u}(t). |
||
</math> |
</math> |
||
Revision as of 16:12, 12 March 2013
The basic idea of almost all the model order reduction (MOR) methods is to
find a subspace 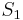 which approximates the manifold where the state
vector Failed to parse (syntax error): {\bf x}(t)
resides. Afterwards, Failed to parse (syntax error): {\bf x}(t)
is approximated by a vector Failed to parse (syntax error): \tilde{\bf x}(t)
in $S_1$. The reduced model is produced by Petrov-Galerkin projection onto a subspace $S_2$, or by Galerkin projection onto the same subspace
which approximates the manifold where the state
vector Failed to parse (syntax error): {\bf x}(t)
resides. Afterwards, Failed to parse (syntax error): {\bf x}(t)
is approximated by a vector Failed to parse (syntax error): \tilde{\bf x}(t)
in $S_1$. The reduced model is produced by Petrov-Galerkin projection onto a subspace $S_2$, or by Galerkin projection onto the same subspace 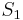 .
.
We use the system Failed to parse (syntax error): E \frac{d{\bf x}}{dt}=A {\bf x}+B {\bf u}(t), Failed to parse (syntax error): {\bf y}(t)=C{\bf x}+D{\bf u}(t).
as an example to explain the basic idea. Assuming that an orthonormal
basis 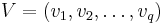 of the subspace
of the subspace 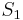 has been
found, then the approximation Failed to parse (syntax error): \tilde{\bf x}(t)
in
has been
found, then the approximation Failed to parse (syntax error): \tilde{\bf x}(t)
in 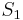 can be represented by
the basis as Failed to parse (syntax error): \tilde{\bf x}(t)=V{\bf z}(t)
. Therefore Failed to parse (syntax error): {\bf x}(t)
can be approximated by Failed to parse (syntax error): {\bf x}(t) \approx V{\bf z}(t)
. Here ${\bf z}$ is a vector
of length $q \ll n$.
can be represented by
the basis as Failed to parse (syntax error): \tilde{\bf x}(t)=V{\bf z}(t)
. Therefore Failed to parse (syntax error): {\bf x}(t)
can be approximated by Failed to parse (syntax error): {\bf x}(t) \approx V{\bf z}(t)
. Here ${\bf z}$ is a vector
of length $q \ll n$.
Once Failed to parse (syntax error): {\bf z}(t) is computed, we can get an approximate solution Failed to parse (syntax error): \tilde{\bf x}(t)=V{\bf z}(t) for Failed to parse (syntax error): {\bf x}(t) . The vector Failed to parse (syntax error): {\bf z}(t) can be computed from the reduced model which is derived by the following two steps.
