(unfortunatly still not finished (some open questions need to be discussed)) |
|||
| Line 10: | Line 10: | ||
==Description== |
==Description== |
||
| − | [[File:Staender_Geom_white.jpg|thumb|120px|CAD Geometry]]The vertical stand represents a structural part of a machine tool. On one of its surfaces there are guide rails located. On these rails a tool slide is moving due to the machining process the slide has to perform by the machine tool on top. The machining process produces a certain amount of heat which is transported through the structure into the vertical stand. This heat source |
+ | [[File:Staender_Geom_white.jpg|thumb|right|120px|CAD Geometry]]The vertical stand represents a structural part of a machine tool. On one of its surfaces there are guide rails located. On these rails a tool slide is moving due to the machining process the slide has to perform by the machine tool on top. The machining process produces a certain amount of heat which is transported through the structure into the vertical stand. This heat source is considered to be a temperature input at the guide rails. This transfered heat amount leads to deformations within the device induced by the prevailed temperature field denoted by <math> x </math>. The evolution of this field is modeled by the heat equation |
| + | <!--How to include a comment? As you can see the question is already the answer.--> |
||
| + | <math> |
||
| + | c_p\rho\frac{\partial{x}}{\partial{t}}=\nabla.(\lambda\nabla x)=0 |
||
| + | </math> |
||
| + | |||
| ⚫ | |||
<math> |
<math> |
||
| − | + | \lambda\frac{\partial x}{\partial n}=\kappa(x-x_{ext}) |
|
| + | </math> on <math> \Gamma_{surf} </math> (remaining boundaries), |
||
| + | |||
| + | describing the heat transfer to the ambience and |
||
| + | |||
| + | <math> |
||
| + | \lambda\frac{\partial x}{\partial n}=q \qquad\qquad\qquad |
||
| ⚫ | |||
| + | |||
| + | which describes the heat transfer between tool slide and vertical stand. |
||
| + | |||
| + | The heat load <math>q</math> induced by the slide and the external temperature <math>x_{ext}</math> serves as the input <math> u </math> of the corresponding state-space system. |
||
| + | |||
| + | |||
| + | The position of the moving slide has been included into the system as a parameter dependency <math> \mu </math>. Due to this motion the region there the input acts on the system is varying and thus one obtains a parameter dependent input matrix |
||
| + | <math> B(\mu) </math>. |
||
| + | |||
| + | Finally, the system describing the heat evolution induced by the moving heat source is given by: |
||
| + | |||
| + | <math> |
||
| + | \begin{array}{lll} |
||
| + | E\dot{x}=Ax+B_{surf}x_{ext}+B_{slide}(\mu)q,\\ |
||
| + | \ \ \quad=Ax+B(\mu)u,\\ |
||
| + | \quad\! y=Cx |
||
| + | \end{array} |
||
</math> |
</math> |
||
| + | ==Data== |
||
| ⚫ | |||
| + | [[File:Matrices_VertStand.tar.gz]] |
||
| ⚫ | |||
| + | The data file consists of the matrices: |
||
| + | <math> |
||
| + | E,A,B_{slide},B_{surf}\in\mathbb{R}^{n\times n} |
||
| + | </math> |
||
| + | and some |
||
| − | <math> \lambda\frac{\partial\theta}{\partial n}\theta=\kappa(\theta-\theta_{ext}) </math> on the remaining boundaries, which describes the heat transfer to the ambience. |
||
==Origins== |
==Origins== |
||
Revision as of 16:07, 14 February 2013
Description
The vertical stand represents a structural part of a machine tool. On one of its surfaces there are guide rails located. On these rails a tool slide is moving due to the machining process the slide has to perform by the machine tool on top. The machining process produces a certain amount of heat which is transported through the structure into the vertical stand. This heat source is considered to be a temperature input at the guide rails. This transfered heat amount leads to deformations within the device induced by the prevailed temperature field denoted by  . The evolution of this field is modeled by the heat equation
. The evolution of this field is modeled by the heat equation
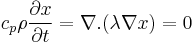
with the boundary conditions
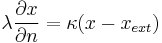 on
on  (remaining boundaries),
(remaining boundaries),
describing the heat transfer to the ambience and
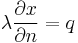 on
on 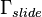 (surface where the tool slide is moving on the guide rails),
(surface where the tool slide is moving on the guide rails),
which describes the heat transfer between tool slide and vertical stand.
The heat load  induced by the slide and the external temperature
induced by the slide and the external temperature 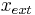 serves as the input
serves as the input  of the corresponding state-space system.
of the corresponding state-space system.
The position of the moving slide has been included into the system as a parameter dependency 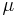 . Due to this motion the region there the input acts on the system is varying and thus one obtains a parameter dependent input matrix
. Due to this motion the region there the input acts on the system is varying and thus one obtains a parameter dependent input matrix
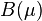 .
.
Finally, the system describing the heat evolution induced by the moving heat source is given by:
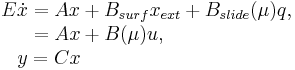
Data
File:Matrices VertStand.tar.gz
The data file consists of the matrices:
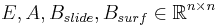
and some
Origins
Contact information:

