Difference between revisions of "Vertical Stand"

Revision as of 14:55, 29 November 2012

Description

The vertical stand represents a structural part of a machine tool. On one of its surfaces there are guide rails located. On these rails a tool slide is moving due to the machining process the slide has to perform by the machine tool on top. The machining process producing a certain amount of heat which is transported through the structure into the vertical stand. This heat source will be considered as an temperature input at the guide rails. This transfered heat amount will lead to deformations within the device induced by the prevailed temperature field. The evolution of this field is modeled by the heat equation

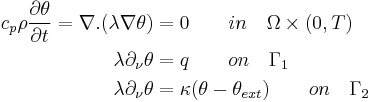
$\begin{align} c_p\rho\frac{\partial{\theta}}{\partial{t}}=\nabla.(\lambda\nabla \theta)&=0\qquad in\quad\Omega\times(0,T)\\ \lambda\partial_\nu \theta&=q \qquad on\quad\Gamma_1\\ \lambda\partial_\nu \theta&=\kappa(\theta-\theta_{ext}) \qquad on\quad\Gamma_2 \end{align}$

Contact information:

Norman Lang

@@ Line 8: / Line 8: @@
 <math>
 \begin{align}
-c_p\rho\frac{\partial{x}}{\partial{t}}=\nabla.(\lambda\nabla x)&=0\qquad in \Omega\times(0,T)\\
+c_p\rho\frac{\partial{\theta}}{\partial{t}}=\nabla.(\lambda\nabla \theta)&=0\qquad in\quad\Omega\times(0,T)\\
-\lambda\partial_\nu x&=q \qquad on \Gamma_s
+\lambda\partial_\nu \theta&=q \qquad on\quad\Gamma_1\\
+\lambda\partial_\nu \theta&=\kappa(\theta-\theta_{ext}) \qquad on\quad\Gamma_2
 \end{align}
 </math>