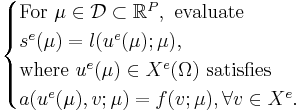| Line 2: | Line 2: | ||
[[Category:parametric method]] |
[[Category:parametric method]] |
||
| − | The Reduced Basis Method we present here is applicable to static and time-dependent linear PDEs. |
+ | The Reduced Basis Method (RBM) we present here is applicable to static and time-dependent linear PDEs. |
==Time-Independent PDEs== |
==Time-Independent PDEs== |
||
| + | |||
| + | The typical model problem of the RBM consists of a parametrized PDE stated in weak form with |
||
| + | bilinear form <math> a(\cdot, \cdot; \mu) </math> and linear form <math> f(\cdot; \mu) </math>. |
||
| + | The parameter <math> \mu </math> is considered within a domain <math> \mathcal{D} </math> |
||
| + | and we are interested in an output quantity <math> s(\mu) </math> which can be |
||
| + | expressed via a linear functional of the field variable <math> l(\cdot; \mu) </math>. |
||
| + | |||
| + | The exact, infinite-dimensional formulation, indicated by the superscript e, is given by |
||
| + | |||
<math> |
<math> |
||
| Line 11: | Line 20: | ||
s^e(\mu) = l(u^e(\mu);\mu), \\ |
s^e(\mu) = l(u^e(\mu);\mu), \\ |
||
\text{where } u^e(\mu) \in X^e(\Omega) \text{ satisfies } \\ |
\text{where } u^e(\mu) \in X^e(\Omega) \text{ satisfies } \\ |
||
| − | a(u^e(\mu),v;\mu) = f(v;\mu), \forall v \in X^e |
+ | a(u^e(\mu),v;\mu) = f(v;\mu), \forall v \in X^e. |
\end{cases} |
\end{cases} |
||
</math> |
</math> |
||
Revision as of 15:09, 19 November 2012
The Reduced Basis Method (RBM) we present here is applicable to static and time-dependent linear PDEs.
Time-Independent PDEs
The typical model problem of the RBM consists of a parametrized PDE stated in weak form with
bilinear form 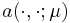 and linear form
and linear form 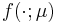 .
The parameter
.
The parameter 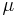 is considered within a domain
is considered within a domain 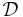 and we are interested in an output quantity
and we are interested in an output quantity 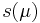 which can be
expressed via a linear functional of the field variable
which can be
expressed via a linear functional of the field variable 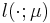 .
.
The exact, infinite-dimensional formulation, indicated by the superscript e, is given by