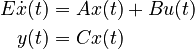(→Data: Update benchmark data files) |
|||
| (15 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
[[Category:Oberwolfach]] |
[[Category:Oberwolfach]] |
||
| + | [[Category:linear]] |
||
| + | [[Category:time invariant]] |
||
| + | [[Category:first differential order]] |
||
| + | [[Category:MIMO]] |
||
| + | [[Category:sparse]] |
||
| + | |||
| + | {{Infobox |
||
| + | |Title = Convective Thermal Flow |
||
| + | |Benchmark ID = |
||
| + | * ctfChipCoolingv0_n20082m1q5 |
||
| + | * ctfChipCoolingv01_n20082m1q5 |
||
| + | * ctfFlowMeterv0_n9669m1q5 |
||
| + | * ctfFlowMeterv05_n9669m1q5 |
||
| + | |Category = oberwolfach |
||
| + | |System-Class = LTI-FOS |
||
| + | |nstates = |
||
| + | * 20082 |
||
| + | * 20082 |
||
| + | * 9669 |
||
| + | * 9669 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 5 |
||
| + | |nparameters = 0 |
||
| + | |components = A, B, C, E |
||
| + | |License = NA |
||
| + | |Creator = C. Moosmann, E.B. Rudnyi, A. Greiner, J.G. Korvink |
||
| + | |Editor = |
||
| + | * [[User:Himpe]] |
||
| + | |Zenodo-link = NA |
||
| + | }} |
||
==Description: Convective Thermal Flow Problems== |
==Description: Convective Thermal Flow Problems== |
||
| Line 12: | Line 40: | ||
However, CFD is computationally expensive. |
However, CFD is computationally expensive. |
||
A popular solution is to exclude the flow completely from the computational domain and to use convection boundary conditions for the solid model. |
A popular solution is to exclude the flow completely from the computational domain and to use convection boundary conditions for the solid model. |
||
| − | However, caution has to be taken to select the film coefficient. |
+ | However, caution has to be taken to select the [[wikipedia:Heat_transfer_coefficient|film coefficient]]. |
| − | An intermediate level is to include a flow region with a given velocity profile |
+ | An intermediate level is to include a flow region with a given velocity profile that adds convective transport to the model. |
| − | Compared to convection boundary conditions this approach has the advantage that the film coefficient |
+ | Compared to convection boundary conditions this approach has the advantage that the film coefficient does not need to be specified and that information about the heat profile in the flow can be obtained. |
| − | A drawback of the method is the greatly increased number of elements needed to perform a physically valid simulation |
+ | A drawback of the method is the greatly increased number of elements needed to perform a physically valid simulation because the solution accuracy when employing upwind finite element schemes depends on the element size. |
While this problem still is linear, due to the forced convection, the conductivity matrix changes from a symmetric matrix to an un-symmetric one. |
While this problem still is linear, due to the forced convection, the conductivity matrix changes from a symmetric matrix to an un-symmetric one. |
||
So this problem type can be used as a benchmark for problems containing un-symmetric matrices. |
So this problem type can be used as a benchmark for problems containing un-symmetric matrices. |
||
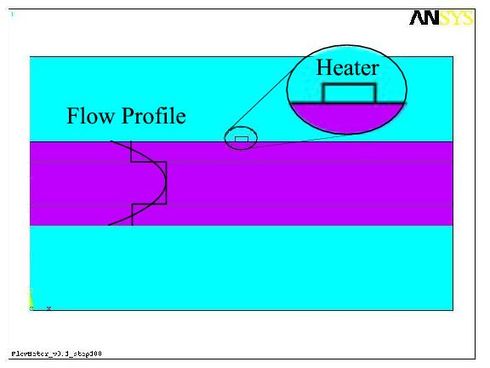
| − | Two different designs are tested: a 2D model of an anemometer-like structure mainly consisting of a tube and a small heat source ( |
+ | Two different designs are tested: a 2D model of an [[Anemometer|anemometer]]-like structure mainly consisting of a tube and a small heat source (Fig. 1) <ref name="ernst2001"/>. |
The solid model has been generated and meshed in [http://www.ansys.com ANSYS]. |
The solid model has been generated and meshed in [http://www.ansys.com ANSYS]. |
||
Triangular <tt>PLANE55</tt> elements have been used for meshing and discretizing by the finite element method, resulting in 19282 elements and 9710 nodes. |
Triangular <tt>PLANE55</tt> elements have been used for meshing and discretizing by the finite element method, resulting in 19282 elements and 9710 nodes. |
||
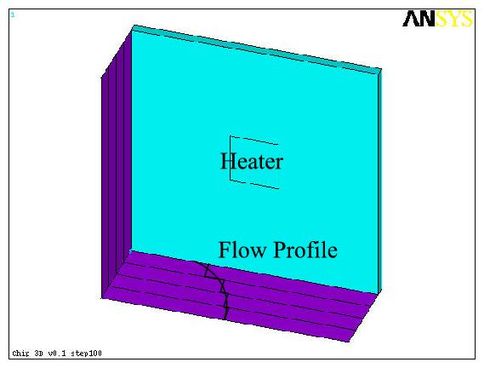
| − | The second design is a 3D model of a chip cooled by forced convection ( |
+ | The second design is a 3D model of a chip cooled by forced convection (Fig. 2) <ref name="harper1997"/>. |
| − | In this case the tetrahedral element type <tt>SOLID70</tt> was used, resulting in 107989 elements and 20542 nodes. |
+ | In this case, the tetrahedral element type <tt>SOLID70</tt> was used, resulting in 107989 elements and 20542 nodes. |
| − | Since the implementation of the convective term in ANSYS does not allow |
+ | Since the implementation of the convective term in ANSYS does not allow defining the fluid speed on a per-element basis but on a per-region one, the flow profile has to be approximated by piece-wise step functions. |
| − | The approximation used for |
+ | The approximation used for these benchmarks is shown in Fig. 1. |
The Dirichlet boundary conditions are applied to the original system. |
The Dirichlet boundary conditions are applied to the original system. |
||
| − | In both models the reference temperature is set to <math>300 K</math>, Dirichlet boundary conditions as well as initial conditions are set to 0 with respect to the reference. |
+ | In both models, the reference temperature is set to <math>300 \, \text{K}</math>, and Dirichlet boundary conditions as well as initial conditions are set to <math>0</math> with respect to the reference. |
| − | The specified Dirichlet boundary conditions are in both cases the inlet of the fluid and the outer faces of the solids. Matrices are supplied for the symmetric case (fluid speed is zero; no convection), and the |
+ | The specified Dirichlet boundary conditions are in both cases the inlet of the fluid and the outer faces of the solids. Matrices are supplied for the symmetric case (fluid speed is zero; no convection), and the non-symmetric case (with forced convection). |
Table 1 shows the output nodes specified for the two benchmarks, Table 2 links the filenames according to the different cases. |
Table 1 shows the output nodes specified for the two benchmarks, Table 2 links the filenames according to the different cases. |
||
| + | |||
| + | Practically, only a few nodes are considered quantities of interest. |
||
| + | Hence, a small subset of five nodes is selected as output nodes, |
||
| + | which are filtered from the discretized state by a linear transformation. |
||
==Origin== |
==Origin== |
||
| Line 114: | Line 146: | ||
|Flow Meter |
|Flow Meter |
||
|<math>0</math> |
|<math>0</math> |
||
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Convection-dim1e4-flow_meter_model_v0.tgz Convection-dim1e4-flow_meter_model_v0.tgz] |
|649.4 kB |
|649.4 kB |
||
|- |
|- |
||
| |
| |
||
|<math>0.5</math> |
|<math>0.5</math> |
||
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Convection-dim1e4-flow_meter_model_v0.5.tgz Convection-dim1e4-flow_meter_model_v0.5.tgz] |
|757.8 kB |
|757.8 kB |
||
|- |
|- |
||
|Cooling Structure |
|Cooling Structure |
||
|<math>0</math> |
|<math>0</math> |
||
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Convection-dim1e4-chip_cooling_model_v0.tgz Convection-dim1e4-chip_cooling_model_v0.tgz] |
|3.9 MB |
|3.9 MB |
||
|- |
|- |
||
| |
| |
||
|<math>0.1</math> |
|<math>0.1</math> |
||
| − | |[https:// |
+ | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Convection-dim1e4-chip_cooling_model_v0.1.tgz Convection-dim1e4-chip_cooling_model_v0.1.tgz] |
|4.0 MB |
|4.0 MB |
||
|} |
|} |
||
| Line 142: | Line 174: | ||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | E \dot{x}(t) &= |
+ | E \dot{x}(t) &= A x(t) + B u(t) \\ |
| − | y(t) &= |
+ | y(t) &= C x(t) |
\end{align} |
\end{align} |
||
</math> |
</math> |
||
| Line 149: | Line 181: | ||
System dimensions: |
System dimensions: |
||
| − | <math>E \in \mathbb{R}^{ |
+ | <math>E \in \mathbb{R}^{n \times n}</math>, |
| − | <math>A \in \mathbb{R}^{ |
+ | <math>A \in \mathbb{R}^{n \times n}</math>, |
| − | <math>B \in \mathbb{R}^{ |
+ | <math>B \in \mathbb{R}^{n \times 1}</math>, |
| − | <math>C \in \mathbb{R}^{5 \times |
+ | <math>C \in \mathbb{R}^{5 \times n}</math>. |
System variants: |
System variants: |
||
| − | <tt>flow_v0</tt>: <math> |
+ | <tt>flow_v0</tt>: <math>n = 9669</math>, |
| − | <tt>flow_v0.5</tt>: <math> |
+ | <tt>flow_v0.5</tt>: <math>n = 9669</math>, |
| − | <tt>chip_v0</tt>: <math> |
+ | <tt>chip_v0</tt>: <math>n = 20082</math>, |
| − | <tt>chip_v0.1</tt>: <math> |
+ | <tt>chip_v0.1</tt>: <math>n = 20082</math>. |
| + | |||
| + | ==Citation== |
||
| + | |||
| + | To cite this benchmark, use the following references: |
||
| + | |||
| + | * For the benchmark itself and its data: |
||
| + | ::The MORwiki Community, '''Convective Thermal Flow'''. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Convective_Thermal_Flow |
||
| + | |||
| + | @MISC{morwiki_convection, |
||
| + | author = <nowiki>{{The MORwiki Community}}</nowiki>, |
||
| + | title = {Convective Thermal Flow}, |
||
| + | howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
||
| + | url = <nowiki>{https://modelreduction.org/morwiki/Convection}</nowiki>, |
||
| + | year = {2018} |
||
| + | } |
||
| + | |||
| + | * For the background on the benchmark: |
||
| + | |||
| + | @INPROCEEDINGS{morMooRGetal04, |
||
| + | author = <nowiki>{C. Moosmann, E.B. Rudnyi, A. Greiner, J.G. Korvink}</nowiki>, |
||
| + | title = {Model Order Reduction for Linear Convective Thermal Flow}, |
||
| + | booktitle = {Proceedings of 10th International Workshops on THERMal INvestigations of ICs and Systems}, |
||
| + | year = {2004}, |
||
| + | url = <nowiki>{http://modelreduction.com/doc/papers/moosmann04THERMINIC.pdf}</nowiki> |
||
| + | } |
||
==References== |
==References== |
||
| Line 173: | Line 230: | ||
<ref name="moosmann2004">C. Moosmann, E.B. Rudnyi, A. Greiner, J.G. Korvink, <span class="plainlinks">[http://modelreduction.com/doc/papers/moosmann04THERMINIC.pdf Model Order Reduction for Linear Convective Thermal Flow]</span>, Proceedings of 10th International Workshops on THERMal INvestigations of ICs and Systems, THERMINIC2004, Sophia Antipolis, France, 2004.</ref> |
<ref name="moosmann2004">C. Moosmann, E.B. Rudnyi, A. Greiner, J.G. Korvink, <span class="plainlinks">[http://modelreduction.com/doc/papers/moosmann04THERMINIC.pdf Model Order Reduction for Linear Convective Thermal Flow]</span>, Proceedings of 10th International Workshops on THERMal INvestigations of ICs and Systems, THERMINIC2004, Sophia Antipolis, France, 2004.</ref> |
||
| − | <ref name="moosmann2005">C. Moosmann, A. Greiner, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_16 Convective Thermal Flow Problems]</span>, |
+ | <ref name="moosmann2005">C. Moosmann, A. Greiner, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_16 Convective Thermal Flow Problems]</span>, In: Dimension Reduction of Large-Scale Systems. Springer, Berlin, Heidelberg. Lecture Notes in Computational Science and Engineering, vol 45: 341--343, 2005.</ref> |
</references> |
</references> |
||
Latest revision as of 09:23, 3 July 2025
| Background | |
|---|---|
| Benchmark ID |
|
| Category |
oberwolfach |
| System-Class |
LTI-FOS |
| Parameters | |
| nstates |
|
| ninputs |
1 |
| noutputs |
5 |
| nparameters |
0 |
| components |
A, B, C, E |
| Copyright | |
| License |
NA |
| Creator |
C. Moosmann, E.B. Rudnyi, A. Greiner, J.G. Korvink |
| Editor | |
| Location | |
|
NA | |
Description: Convective Thermal Flow Problems
Many thermal problems require simulation of heat exchange between a solid body and a fluid flow. The most elaborate approach to this problem is computational fluid dynamics (CFD). However, CFD is computationally expensive. A popular solution is to exclude the flow completely from the computational domain and to use convection boundary conditions for the solid model. However, caution has to be taken to select the film coefficient.
An intermediate level is to include a flow region with a given velocity profile that adds convective transport to the model. Compared to convection boundary conditions this approach has the advantage that the film coefficient does not need to be specified and that information about the heat profile in the flow can be obtained. A drawback of the method is the greatly increased number of elements needed to perform a physically valid simulation because the solution accuracy when employing upwind finite element schemes depends on the element size. While this problem still is linear, due to the forced convection, the conductivity matrix changes from a symmetric matrix to an un-symmetric one. So this problem type can be used as a benchmark for problems containing un-symmetric matrices.
Two different designs are tested: a 2D model of an anemometer-like structure mainly consisting of a tube and a small heat source (Fig. 1) [1]. The solid model has been generated and meshed in ANSYS. Triangular PLANE55 elements have been used for meshing and discretizing by the finite element method, resulting in 19282 elements and 9710 nodes. The second design is a 3D model of a chip cooled by forced convection (Fig. 2) [2]. In this case, the tetrahedral element type SOLID70 was used, resulting in 107989 elements and 20542 nodes. Since the implementation of the convective term in ANSYS does not allow defining the fluid speed on a per-element basis but on a per-region one, the flow profile has to be approximated by piece-wise step functions. The approximation used for these benchmarks is shown in Fig. 1.
The Dirichlet boundary conditions are applied to the original system.
In both models, the reference temperature is set to 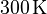 , and Dirichlet boundary conditions as well as initial conditions are set to
, and Dirichlet boundary conditions as well as initial conditions are set to 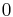 with respect to the reference.
The specified Dirichlet boundary conditions are in both cases the inlet of the fluid and the outer faces of the solids. Matrices are supplied for the symmetric case (fluid speed is zero; no convection), and the non-symmetric case (with forced convection).
Table 1 shows the output nodes specified for the two benchmarks, Table 2 links the filenames according to the different cases.
with respect to the reference.
The specified Dirichlet boundary conditions are in both cases the inlet of the fluid and the outer faces of the solids. Matrices are supplied for the symmetric case (fluid speed is zero; no convection), and the non-symmetric case (with forced convection).
Table 1 shows the output nodes specified for the two benchmarks, Table 2 links the filenames according to the different cases.
Practically, only a few nodes are considered quantities of interest. Hence, a small subset of five nodes is selected as output nodes, which are filtered from the discretized state by a linear transformation.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[3]; No. 38867, see [4].
Data
Matrices are in the Matrix Market format. The matrix name is used as an extension of the matrix file. *.C.names contains a list of output names written consecutively. The system matrices have been extracted from ANSYS models by means of mor4fem.
| Model | Number | Code | Comment |
|---|---|---|---|
| Flow Meter | 1 | out1 | outlet position |
| 2 | out2 | outlet position | |
| 3 | SenL | left sensor position | |
| 4 | Heater | within the heater | |
| 5 | SenR | right sensor position | |
| Cooling Structure | 1 | out1 | outlet position |
| 2 | out2 | outlet position | |
| 3 | out3 | outlet position | |
| 4 | out4 | outlet position | |
| 5 | Heater | within the heater |
| Model | Fluid Speed (m/s) | Link | Size |
|---|---|---|---|
| Flow Meter | 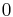
|
Convection-dim1e4-flow_meter_model_v0.tgz | 649.4 kB |
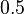
|
Convection-dim1e4-flow_meter_model_v0.5.tgz | 757.8 kB | |
| Cooling Structure | 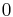
|
Convection-dim1e4-chip_cooling_model_v0.tgz | 3.9 MB |
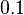
|
Convection-dim1e4-chip_cooling_model_v0.1.tgz | 4.0 MB |
Further information on the models can be found in [5], where model reduction by means of the Arnoldi algorithm is also presented.
Dimensions
System structure:
System dimensions:
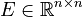 ,
,
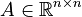 ,
,
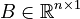 ,
,
 .
.
System variants:
flow_v0: 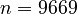 ,
flow_v0.5:
,
flow_v0.5: 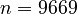 ,
chip_v0:
,
chip_v0: 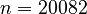 ,
chip_v0.1:
,
chip_v0.1: 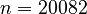 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Convective Thermal Flow. MORwiki - Model Order Reduction Wiki, 2018. http://modelreduction.org/index.php/Convective_Thermal_Flow
@MISC{morwiki_convection,
author = {{The MORwiki Community}},
title = {Convective Thermal Flow},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Convection},
year = {2018}
}
- For the background on the benchmark:
@INPROCEEDINGS{morMooRGetal04,
author = {C. Moosmann, E.B. Rudnyi, A. Greiner, J.G. Korvink},
title = {Model Order Reduction for Linear Convective Thermal Flow},
booktitle = {Proceedings of 10th International Workshops on THERMal INvestigations of ICs and Systems},
year = {2004},
url = {http://modelreduction.com/doc/papers/moosmann04THERMINIC.pdf}
}
References
- ↑ H. Ernst, High-Resolution Thermal Measurements in Fluids, PhD thesis, University of Freiburg, Germany, 2001.
- ↑ C.A. Harper, Electronic packaging and interconnection handbook, New York McGraw- Hill, USA, 1997
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ C. Moosmann, A. Greiner, Convective Thermal Flow Problems, In: Dimension Reduction of Large-Scale Systems. Springer, Berlin, Heidelberg. Lecture Notes in Computational Science and Engineering, vol 45: 341--343, 2005.
- ↑ C. Moosmann, E.B. Rudnyi, A. Greiner, J.G. Korvink, Model Order Reduction for Linear Convective Thermal Flow, Proceedings of 10th International Workshops on THERMal INvestigations of ICs and Systems, THERMINIC2004, Sophia Antipolis, France, 2004.