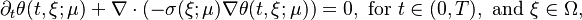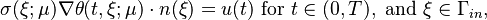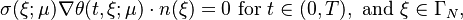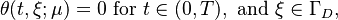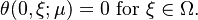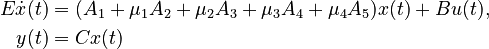(→Discretization: Python capitalization) |
|||
| (17 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
[[Category:parametric]] |
[[Category:parametric]] |
||
| Line 7: | Line 5: | ||
[[Category:first differential order]] |
[[Category:first differential order]] |
||
[[Category:time invariant]] |
[[Category:time invariant]] |
||
| − | [[Category:parametric 2-5 parameters]] |
||
[[Category:MIMO]] |
[[Category:MIMO]] |
||
[[Category:Sparse]] |
[[Category:Sparse]] |
||
| + | |||
| + | {{Infobox |
||
| + | |Title = Thermal Block |
||
| + | |Benchmark ID = thermalBlock_n7488m1q4 |
||
| + | |Category = misc |
||
| + | |System-Class = AP-LTI-FOS |
||
| + | |nstates = 7488 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 4 |
||
| + | |nparameters = 4 |
||
| + | |components = A, B, C, E |
||
| + | |License = BSD 2-Clause "Simplified" License |
||
| + | |Creator = [[User:Saak]] |
||
| + | |Editor = |
||
| + | * [[User:Saak]] |
||
| + | * [[User:Himpe]] |
||
| + | * [[User:Mlinaric]] |
||
| + | |Zenodo-link = https://zenodo.org/record/3691894/files/ABCE.mat |
||
| + | }} |
||
==Description== |
==Description== |
||
| − | A parametric semi-discretized heat transfer problem with varying heat transfer coefficients, the parameters, on subdomains. |
+ | A parametric semi-discretized heat transfer problem with varying heat transfer coefficients, the parameters, on subdomains. This model is also called the ''cookie baking problem'', and can be viewed as a flattened 2-D version of the ''skyscraper problem'' from high-performance computing. |
| + | |||
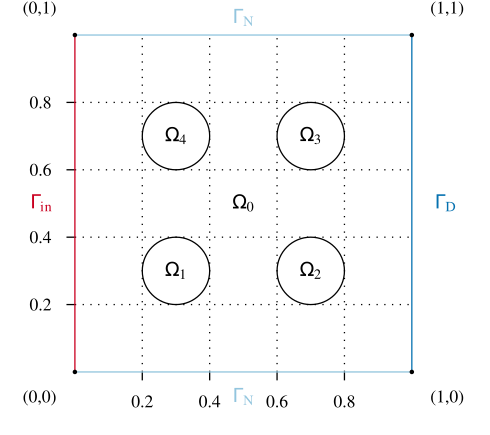
<figure id="fig1">[[File:ThermalBlockDomain.svg|490px|thumb|right|<caption>The computational domain and boundaries.</caption>]]</figure> |
<figure id="fig1">[[File:ThermalBlockDomain.svg|490px|thumb|right|<caption>The computational domain and boundaries.</caption>]]</figure> |
||
<figure id="fig1">[[File:ThermalBlockTend.png|490px|thumb|right|<caption>A sample heat distribution at time 1.0 for parameter choice [100, 0.01, 0.001, 0.0001].</caption>]]</figure> |
<figure id="fig1">[[File:ThermalBlockTend.png|490px|thumb|right|<caption>A sample heat distribution at time 1.0 for parameter choice [100, 0.01, 0.001, 0.0001].</caption>]]</figure> |
||
| Line 41: | Line 58: | ||
===Discretization=== |
===Discretization=== |
||
| − | For the discretization, [https://fenicsproject.org/ |
+ | For the discretization, [https://fenicsproject.org/ FEniCS] '''2019.1''' was used on a simplicial grid with first order elements. The mesh is generated from the domain specification using [http://gmsh.info/ gmsh] '''3.0.6''' with '<code>clscale</code>' set to <math>0.1</math>. The Python-based source code for the discretization can be found at [https://doi.org/10.5281/zenodo.3691894 Zenodo]. |
==Origin== |
==Origin== |
||
| Line 47: | Line 64: | ||
==Data== |
==Data== |
||
| − | The benchmark includes the basic domain description as a gmsh input file, Python scripts for the matrix assembly, simulation in pyMOR and visualization as VTK, together with the matrices both as one combined file <code>ABCE.mat</code> or separate matrix market files for all matrices. The sources and the <code>ABCE.mat</code> are available for download at [https://doi.org/10.5281/zenodo.3691894 Zenodo]. |
+ | The benchmark includes the basic domain description as a gmsh input file, Python scripts for the matrix assembly, simulation in pyMOR, and visualization as VTK, together with the matrices both as one combined file <code>ABCE.mat</code> or separate matrix market files for all matrices. The sources and the <code>ABCE.mat</code> are available for download at [https://doi.org/10.5281/zenodo.3691894 Zenodo]. |
Note that the heat transfer coefficients are designed as characteristic functions on the domains, such that the system is only well-posed when all entries in <math>\mu</math> are positive. |
Note that the heat transfer coefficients are designed as characteristic functions on the domains, such that the system is only well-posed when all entries in <math>\mu</math> are positive. |
||
| Line 55: | Line 72: | ||
:<math> |
:<math> |
||
\begin{align} |
\begin{align} |
||
| − | E\dot{x}(t) &= ( |
+ | E\dot{x}(t) &= (A_1 + \mu_1 A_2 + \mu_2 A_3 + \mu_3 A_4 + \mu_4 A_5) x(t) + Bu(t), \\ |
y(t) &= Cx(t) |
y(t) &= Cx(t) |
||
\end{align} |
\end{align} |
||
| Line 64: | Line 81: | ||
<math>E \in \mathbb{R}^{N \times N}</math>, |
<math>E \in \mathbb{R}^{N \times N}</math>, |
||
| − | <math> |
+ | <math>A_{1,...,5} \in \mathbb{R}^{N \times N}</math>, |
| − | <math>A_1 \in \mathbb{R}^{N \times N}</math>, |
||
| − | <math>A_2 \in \mathbb{R}^{N \times N}</math>, |
||
| − | <math>A_3 \in \mathbb{R}^{N \times N}</math>, |
||
| − | <math>A_4 \in \mathbb{R}^{N \times N}</math>, |
||
<math>B \in \mathbb{R}^{N \times 1}</math>, |
<math>B \in \mathbb{R}^{N \times 1}</math>, |
||
<math>C \in \mathbb{R}^{4 \times N}</math>, |
<math>C \in \mathbb{R}^{4 \times N}</math>, |
||
| Line 75: | Line 88: | ||
==Variants== |
==Variants== |
||
| − | Besides the full four parameter setup, the model can be used in variations with other numbers of independent parameters. The following two are recommended in the original work and have been investigated in the literature<ref name="morBenW20c"/>,<ref name="morHim20"/>,<ref name="morBenKS20"/>. |
+ | Besides the full four parameter setup, the model can be used in variations with other numbers of independent parameters. The following two are recommended in the original work and have been investigated in the literature<ref name="morBenW20c"/>,<ref name="morHim20"/>,<ref name="morBenKS20"/>,<ref name="morMliRS20"/>. |
===Single parameter=== |
===Single parameter=== |
||
| − | The interpretation of the thermal block as the "cookie |
+ | The interpretation of the thermal block as the "cookie baking" problem with slight variation in the dough leads to an easy one parameter variant. Here the new single parameter <math>\hat\mu\in [ 10^{-6}, 10^2]</math> is chosen such that <math> \mu = \hat\mu\left[0.2, 0.4, 0.6, 0.8\right]. </math> |
===Non-parametric=== |
===Non-parametric=== |
||
| − | The system can be used as a standard LTI state-space model. It is |
+ | The system can be used as a standard LTI state-space model. It is suggested to use <math>\mu = \sqrt{10} [0.2, 0.4, 0.6, 0.8]</math>. |
==Citation== |
==Citation== |
||
| Line 87: | Line 100: | ||
* For the benchmark itself and its data: |
* For the benchmark itself and its data: |
||
| − | :: S. Rave and J. Saak, '''Thermal Block'''. MORwiki - Model Order Reduction Wiki, 2020. |
+ | :: S. Rave and J. Saak, '''Thermal Block'''. MORwiki - Model Order Reduction Wiki, 2020. https://modelreduction.org/morwiki/Thermal_Block |
@MISC{morwiki_thermalblock, |
@MISC{morwiki_thermalblock, |
||
| Line 93: | Line 106: | ||
title = {Thermal Block}, |
title = {Thermal Block}, |
||
howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
||
| − | url = <nowiki>{ |
+ | url = <nowiki>{https://modelreduction.org/morwiki/Thermal_Block}</nowiki>, |
year = 2020 |
year = 2020 |
||
} |
} |
||
* For the background on the benchmark: |
* For the background on the benchmark: |
||
| − | :: S. Rave and J. Saak, <span class="plainlinks">[https://arxiv.org/abs/2003.00846 ''' |
+ | :: S. Rave and J. Saak, <span class="plainlinks">[https://arxiv.org/abs/2003.00846 '''A Non-Stationary Thermal-Block Benchmark Model for Parametric Model Order Reduction''']. e-prints 2003.00846, arXiv, math.NA (2020). |
| + | @INPROCEEDINGS{morRavS21, |
||
| − | @TECHREPORT{morRavS20, |
||
author = {Rave, S. and Saak, J.}, |
author = {Rave, S. and Saak, J.}, |
||
| − | title = { |
+ | title = {A Non-Stationary Thermal-Block Benchmark Model for Parametric Model Order Reduction}, |
| + | booktitle = {Model Reduction of Complex Dynamical Systems}, |
||
| − | Model Order Reduction}, |
||
| + | series = {International Series of Numerical Mathematics}, |
||
| − | institution = {arXiv}, |
||
| − | + | volume = {171}, |
|
| − | + | publisher = {Springer}, |
|
| − | + | year = 2021, |
|
| − | + | doi = {10.1007/978-3-030-72983-7_16} |
|
| − | url = <nowiki>{https://arxiv.org/abs/2003.00846}</nowiki> |
||
} |
} |
||
==References== |
==References== |
||
<references> |
<references> |
||
| − | <ref name="morBenW20c">P. Benner, S. W. R. Werner, <span class="plainlinks">[https:// |
+ | <ref name="morBenW20c">P. Benner, S. W. R. Werner, <span class="plainlinks">[https://doi.org/10.1007/978-3-030-72983-7_19 MORLAB -- the Model Order Reduction LABoratory]</span>, |
| + | Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 393--415, 2021.</ref> |
||
| − | e-print 2002.12682, arXiv, cs.MS (2020).</ref> |
||
| − | <ref name="morHim20">C. Himpe, <span class="plainlinks">[https:// |
+ | <ref name="morHim20">C. Himpe, <span class="plainlinks">[https://doi.org/10.1007/978-3-030-72983-7_7 Comparing (empirical-Gramian-based) model order reduction algorithms]</span>, |
| + | Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 141--164, 2021.</ref> |
||
| − | <ref name="morBenKS20">P. Benner, M. Köhler, J. Saak, <span class="plainlinks">[https://arxiv.org/abs/2003.02088 Matrix equations, sparse solvers: M-M.E.S.S.-2.0.1 – philosophy, features and application for (parametric) model order reduction]</span>, eprints 2003.02088, arXiv, cs.MS (2020).</ref> |
||
| − | <ref name=" |
+ | <ref name="morBenKS20">P. Benner, M. Köhler, J. Saak, <span class="plainlinks">[https://doi.org/10.1007/978-3-030-72983-7_18 Matrix equations, sparse solvers: M-M.E.S.S.-2.0.1 – philosophy, features and application for (parametric) model order reduction]</span>, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 369--392, 2021.</ref> |
| + | <ref name="morRavS20">S. Rave, J. Saak, <span class="plainlinks">[https://doi.org/10.1007/978-3-030-72983-7_16 An Non-Stationary Thermal-Block Benchmark Model for Parametric Model Order Reduction]</span>, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 349-356, 2021.</ref> |
||
| − | </references> |
||
| + | <ref name="morMliRS20">P. Mlinarić, S. Rave, J. Saak, <span class="plainlinks">[https://doi.org/10.1007/978-3-030-72983-7_17 Parametric model order reduction using pyMOR]</span>, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 357--367 , 2021.</ref> |
||
| + | </references> |
||
==Contact== |
==Contact== |
||
Latest revision as of 06:41, 17 June 2025
| Background | |
|---|---|
| Benchmark ID |
thermalBlock_n7488m1q4 |
| Category |
misc |
| System-Class |
AP-LTI-FOS |
| Parameters | |
| nstates |
7488
|
| ninputs |
1 |
| noutputs |
4 |
| nparameters |
4 |
| components |
A, B, C, E |
| Copyright | |
| License |
BSD 2-Clause "Simplified" License |
| Creator | |
| Editor | |
| Location | |
Description
A parametric semi-discretized heat transfer problem with varying heat transfer coefficients, the parameters, on subdomains. This model is also called the cookie baking problem, and can be viewed as a flattened 2-D version of the skyscraper problem from high-performance computing.
Modeling
Consider a parameter ![\mu\in{[10^{-6},10^2]}^4\subset\mathbb{R}^{4}](/morwiki/images/math/b/0/5/b055bfc56b41ae34dc4343ace56270d7.png) and define the heat conductivity
and define the heat conductivity 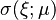 as
as 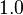 when
when 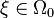 and
and 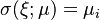 when
when 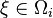 . The heat distribution is governed by the equation:
. The heat distribution is governed by the equation:
with a heat-inflow condition on the left (Neumann boundary)
perfect isolation on the top and bottom (Neumann-zero boundary)
and fixed temperature on the right (Dirichlet boundary)
and initial condition
Discretization
For the discretization, FEniCS 2019.1 was used on a simplicial grid with first order elements. The mesh is generated from the domain specification using gmsh 3.0.6 with 'clscale' set to 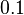 . The Python-based source code for the discretization can be found at Zenodo.
. The Python-based source code for the discretization can be found at Zenodo.
Origin
This benchmark was developed for the MODRED 2019 proceedings[1].
Data
The benchmark includes the basic domain description as a gmsh input file, Python scripts for the matrix assembly, simulation in pyMOR, and visualization as VTK, together with the matrices both as one combined file ABCE.mat or separate matrix market files for all matrices. The sources and the ABCE.mat are available for download at Zenodo.
Note that the heat transfer coefficients are designed as characteristic functions on the domains, such that the system is only well-posed when all entries in 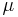 are positive.
are positive.
Dimensions
System structure:
System dimensions:
 ,
,
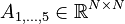 ,
,
 ,
,
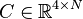 ,
,
where 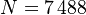 for the system matrices given in
for the system matrices given in ABCE.mat.
Variants
Besides the full four parameter setup, the model can be used in variations with other numbers of independent parameters. The following two are recommended in the original work and have been investigated in the literature[2],[3],[4],[5].
Single parameter
The interpretation of the thermal block as the "cookie baking" problem with slight variation in the dough leads to an easy one parameter variant. Here the new single parameter ![\hat\mu\in [ 10^{-6}, 10^2]](/morwiki/images/math/7/8/e/78e442ccec98fe42c3cfe7078f053362.png) is chosen such that
is chosen such that ![\mu = \hat\mu\left[0.2, 0.4, 0.6, 0.8\right].](/morwiki/images/math/9/1/0/91066c3fba0a3c4e85098ec997d69808.png)
Non-parametric
The system can be used as a standard LTI state-space model. It is suggested to use ![\mu = \sqrt{10} [0.2, 0.4, 0.6, 0.8]](/morwiki/images/math/1/f/5/1f51fe6509b6d6a5867b008afdbb1a10.png) .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- S. Rave and J. Saak, Thermal Block. MORwiki - Model Order Reduction Wiki, 2020. https://modelreduction.org/morwiki/Thermal_Block
@MISC{morwiki_thermalblock,
author = {Rave, S. and Saak, J.},
title = {Thermal Block},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Thermal_Block},
year = 2020
}
- For the background on the benchmark:
- S. Rave and J. Saak, A Non-Stationary Thermal-Block Benchmark Model for Parametric Model Order Reduction. e-prints 2003.00846, arXiv, math.NA (2020).
@INPROCEEDINGS{morRavS21,
author = {Rave, S. and Saak, J.},
title = {A Non-Stationary Thermal-Block Benchmark Model for Parametric Model Order Reduction},
booktitle = {Model Reduction of Complex Dynamical Systems},
series = {International Series of Numerical Mathematics},
volume = {171},
publisher = {Springer},
year = 2021,
doi = {10.1007/978-3-030-72983-7_16}
}
References
- ↑ S. Rave, J. Saak, An Non-Stationary Thermal-Block Benchmark Model for Parametric Model Order Reduction, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 349-356, 2021.
- ↑ P. Benner, S. W. R. Werner, MORLAB -- the Model Order Reduction LABoratory, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 393--415, 2021.
- ↑ C. Himpe, Comparing (empirical-Gramian-based) model order reduction algorithms, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 141--164, 2021.
- ↑ P. Benner, M. Köhler, J. Saak, Matrix equations, sparse solvers: M-M.E.S.S.-2.0.1 – philosophy, features and application for (parametric) model order reduction, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 369--392, 2021.
- ↑ P. Mlinarić, S. Rave, J. Saak, Parametric model order reduction using pyMOR, Model Reduction of Complex Dynamical Systems, International Series of Numerical Mathematics 171: 357--367 , 2021.