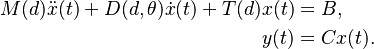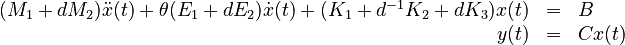| (87 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | [[Category: |
+ | [[Category:benchmark]] |
| + | [[Category:ODE]] |
||
| + | [[Category:linear]] |
||
| + | [[Category:Parametric]] |
||
| + | [[Category:affine parameter representation]] |
||
| + | [[Category:time invariant]] |
||
| + | [[Category:second differential order]] |
||
| + | {{Infobox |
||
| − | ==Description of the device== |
||
| + | |Title = Modified Gyroscope |
||
| − | The device is a MEMS gyroscope based on the butterfly gyroscope[1]developed at the Imego institute in Gothenburg, Sweden (see also: http://simulation.uni-freiburg.de/downloads/benchmark/The Butterfly Gyro (35889)). A gyroscope is a device used to measure angular rates in up to three axes. |
||
| + | |Benchmark ID = modifiedGyroscope_n17931m1q1 |
||
| + | |Category = misc |
||
| + | |System-Class = AP-LTI-SOS |
||
| + | |nstates = 17931 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 1 |
||
| + | |nparameters = 3 |
||
| + | |components = B, C, E, K, M |
||
| + | |License = NA |
||
| + | |Creator = [[User:Feng]] |
||
| + | |Editor = |
||
| + | * [[User:Feng]] |
||
| + | * [[User:Himpe]] |
||
| + | * [[User:Will]] |
||
| + | * [[User:Saak]] |
||
| + | * [[User:Lund]] |
||
| + | |Zenodo-link = NA |
||
| + | }} |
||
| + | ==Description== |
||
| − | The basic working principle of the gyroscope can be describes as follows[2]. Without applied external rotation, the paddles vibrate in phase |
||
| + | <figure id="fig:gyro">[[File:Gyroscope.jpg|300px|thumb|right|<caption>Schematic representation of the gyroscope.</caption>]]</figure> |
||
| − | with the function z(t ). Under the influence of an external rotation about the x-axis (drawn |
||
| − | in red), an additional force due to the Coriolis acceleration acts upon the |
||
| − | paddles. This force leads to an additional small out-of-phase vibration |
||
| − | between two paddles on the same side of the bearing. This |
||
| − | out-of phase vibration is measured as the difference of the z-displacement |
||
| − | of the nodes with the red dots. Thus, measuring the displacement of two |
||
| − | adjacent paddles, the rotation velocity can be ascertained. |
||
| + | The device is a [[wikipedia:Vibrating_structure_gyroscope#MEMS_gyroscopes|MEMS gyroscope]] based on the butterfly gyroscope <ref name="lienemann2004"/> developed at the [http://www.imego.com/ Imego institute] in Gothenburg, |
||
| − | ==Motivation of MOR== |
||
| + | Sweden (see also: [[Butterfly_Gyroscope|Butterfly Gyroscope]], where a non-parametrized model for the device is given). |
||
| + | A [[wikipedia:Gyroscope|gyroscope]] is a device used to measure angular rates in up to three axes. |
||
| + | The basic working principle of the '''gyroscope''' can be described as follows, see also <ref name="Moo07"/>. |
||
| − | When planning for and making decisions on future improvements of the Butterfly Gyroscope, it is of importance to improve the efficiency of the gyro simulations. Repeated analysis of the sensor structure have to be conducted with respect to a number of important issues. Examples of such are sensitivity to shock, linear and angular vibration sensitivity, reaction to large rates and/or acceleration, different types of excitation load cases and the effect of force-feedback. The use of model order reduction indeed decreases run time for repeated simulations. |
||
| + | Without applied external rotation, the paddles vibrate in phase with the function <math>z(t),</math> see Fig. 1. |
||
| + | Under the influence of an external rotation about the <math>x</math>-axis (drawn in red), |
||
| + | an additional force due to the Coriolis acceleration acts upon the paddles. |
||
| + | This force leads to an additional small out-of-phase vibration between two paddles on the same side of the bearing. |
||
| + | This out-of phase vibration is measured as the difference of the <math>z</math>-displacement of the nodes with the red dots. |
||
| + | Thus, measuring the displacement of two adjacent paddles, the rotation velocity can be ascertained. |
||
| + | ==Motivation== |
||
| + | When planning for and making decisions on future improvements of the butterfly gyroscope, it is of importance to improve the efficiency of the gyro simulations. Repeated analysis of the sensor structure have to be conducted with respect to a number of important issues. |
||
| + | Examples of such are sensitivity to shock, linear and angular vibration sensitivity, reaction to large rates and/or acceleration, |
||
| + | different types of excitation load cases and the effect of force-feedback. |
||
| + | The use of model order reduction indeed decreases run time for repeated simulations. |
||
| + | ==The Parametrized Model== |
||
| − | ==Description of the parametrized model== |
||
| − | Two parameters are of special interest for the model. |
+ | Two parameters are of special interest for the model. |
| − | quantity that is to be sensed, the rotation velocity around the x-axes. |
+ | The first one is the quantity that is to be sensed, the rotation velocity <math>\theta</math> around the <math>x</math>-axes. |
| − | The second parameter is the width of the bearing, d. |
+ | The second parameter is the width of the bearing, <math>d</math>. |
| − | The parametrized system below is obtained by |
+ | The parametrized system below is obtained by finite element discretization of the parametrized model (in the form of partial differential equations) for the '''gyroscope'''. |
| − | + | The details of constructing the parametrized system can be found in <ref name="Moo07"/>. |
|
| + | The system is of the following form: |
||
| − | form: |
||
| + | |||
| − | <math> |
||
| + | :<math> |
||
| − | M(d)\ddot{x}+D(\theta)\dot{x}+T(d)x=B |
||
| + | \begin{align} |
||
| − | y=Cx. |
||
| + | M(d)\ddot{x}(t) +D(d,\theta)\dot{x}(t) +T(d)x(t) &= B, \\ |
||
| + | y(t) &=Cx(t). |
||
| + | \end{align} |
||
</math> |
</math> |
||
| − | Here, |
+ | Here, |
| − | <math>M(d)=(M_1+dM_2)\in \mathbb R^{n\times n}</math>is the mass matrix, |
||
| − | <math> |
+ | * <math>M(d)=M_1 + dM_2\in \mathbb R^{n\times n}</math> is the mass matrix, |
| + | * <math>D(d,\theta)=\theta(D_1 + d D_2)\in \mathbb R^{n\times n}</math> is the damping matrix, |
||
| + | * <math>T(d)=T_1+(1/d)T_2+dT_3\in \mathbb R^{n\times n}</math> is the stiffness matrix, |
||
| + | * <math>B \in \mathbb R^{n \times 1}</math> is the load vector, |
||
| + | * <math>C \in \mathbb R^{1 \times n}</math> is the output matrix, |
||
| + | * <math>x \in \mathbb R^{n}</math> is the state vector, |
||
| + | * and <math>y \in \mathbb R </math> is the output response. |
||
| + | The quantity of interest <math>y</math> of the system is <math>\delta z(t)</math>, which is the difference of the displacement <math>z(t)</math> between the two red markings on the ''east'' side of the bearing (see <xr id="fig:gyro"/>). |
||
| − | <math>T(d)=T_1+(1/d)T_2+dT_3\in \mathbb R^{n\times n}</math> is the stiffness matrix, |
||
| + | The parameters of the system, <math>d</math> and <math>\theta</math>, represent the width of the bearing(<math>d</math>) and the rotation velocity along the <math>x</math>-axis (<math>\theta</math>), with the ranges: <math>\theta\in [10^{-7}, 10^{-5}]</math> and <math>d\in [1,2]</math>. |
||
| − | + | The device works in the frequency range <math>f \in [0.025, 0.25]</math>MHz and the degrees of freedom are <math>n = 17913</math>. |
|
| + | ==Data== |
||
| + | The model is generated in ANSYS. |
||
| − | The variables <math>d, \theta</math> are the parameters of the system. |
||
| + | The system matrices <math>M_1, \, M_2, \, D_1, \, D_2, \, T_1, \, T_2, \, T_3</math>, and <math> B</math> are in the [http://math.nist.gov/MatrixMarket/ MatrixMarket format], and can be downloaded here: [[Media: Gyroscope_modi.tgz|Gyroscope_modi.tgz]]. The matrix <math>C</math> defines the output, which has zeros on all the entries, except on the 2315th entry, where the value is <math>-1</math>, and on the 5806th entry, the value is <math>1</math>; |
||
| − | <math>d</math> is the width of the |
||
| + | in MATLAB notation, it is <tt>C(1,2315) = -1</tt> and <tt>C(1,5806) = 1</tt>. |
||
| − | bearing, <math>\theta</math> is the rotation velocity along the <math>x</math> axis. |
||
| + | The matrices have been reindexed for [[MORB]], as shown in the next section. In particular, <math>D_i</math> is denoted instead by <math>E_i</math>, and <math>T_i</math> by <math>K_i</math>. |
||
| + | ==Dimensions== |
||
| − | The interesting output <math>y</math> of the system is <math>\delta</math> which is the |
||
| − | difference of the displacement <math>z(t)</math> between the two red dots on |
||
| − | the same side of the bearing (see Fig.1). The degrees of freedom is <math>n=17913</math>. |
||
| + | System structure: |
||
| + | :<math> |
||
| − | The interesting range for the parameters are: <math>\theta\in [10^{-7}, 10^{-5}]</math>, and <math>d\in [1,2]</math>. The device works in the frequency range <math>f\in [0.025, 0.25]</math>MHz. Typical values of the damping variables <math>\alpha, \beta</math> are <math>0</math> and <math>10^{-6}</math>respectively. It has been proven by Salimbahrami [3]that the matrices associated with the damping variables do not have to be taken into account during the process of model reduction. |
||
| + | \begin{array}{rcl} |
||
| + | (M_1 + d M_2)\ddot{x}(t) + \theta(E_1 + d E_2) \dot{x}(t) + (K_1 + d^{-1} K_2 + d K_3)x(t) &=& B \\ |
||
| + | y(t) &=& Cx(t) |
||
| + | \end{array} |
||
| + | </math> |
||
| + | System dimensions: |
||
| − | ==Data information== |
||
| + | <math>M_{1,2}, E_{1,2}, K_{1,2,3} \in \mathbb{R}^{17931 \times 17931}</math>, |
||
| − | The systems matrices<math>M_1, M_2, D_1, D_2</math>, and <math>T_1, T_2, T_3</math> are in the MatrixMarket (http://math.nist.gov/MatrixMarket/) format, and can be downloaded [[File:matrices.tgz]]. <math>M_1</math> corresponds to the file Bmass1.dat, <math>M_2</math> corresponds to the file Bmass2.dat. <math>D_1, D_2</math> correspond to the files Bdamp1.dat, Bdamp2.dat respectively. <math>T_1, T_2, T_3</math> correspond to the files Bstiff1.dat, Bstiff2.dat, Bstiff3.dat respectively. |
||
| + | <math>B \in \mathbb{R}^{17931 \times 1}</math>, |
||
| − | The load vector <math>B</math> is obtained from the file Bload.dat. |
||
| + | <math>C \in \mathbb{R}^{1 \times 17931}</math>. |
||
| + | |||
| + | ==Citation== |
||
| + | |||
| + | To cite this benchmark, use the following references: |
||
| + | |||
| + | * For the benchmark itself and its data: |
||
| + | ::The MORwiki Community, '''Modified Gyroscope'''. MORwiki - Model Order Reduction Wiki, 2018. https://modelreduction.org/morwiki/Modified_Gyroscope |
||
| + | |||
| + | @MISC{morwiki_modgyro, |
||
| + | author = <nowiki>{{The MORwiki Community}}</nowiki>, |
||
| + | title = {Modified Gyroscope}, |
||
| + | howpublished = {{MORwiki} -- Model Order Reduction Wiki}, |
||
| + | url = <nowiki>{https://modelreduction.org/morwiki/Modified_Gyroscope}</nowiki>, |
||
| + | year = 2018 |
||
| + | } |
||
| + | |||
| + | * For the background on the benchmark: <span class="plainlinks">[https://morwiki.mpi-magdeburg.mpg.de/BibTeX/#morMoo07 morMoo07]</span> (<span class="plainlinks">[https://morwiki.mpi-magdeburg.mpg.de/BibTeX/html/mor_bib.html#morMoo07 BibTeX]</span>) |
||
==References== |
==References== |
||
| + | <references> |
||
| − | [1]Lienemann, D. Billger, E. B. Rudnyi, A. G. iner, J. G. Korvink, ``MEMS |
||
| + | |||
| − | compact modeling meets model order reduction: Examples of the |
||
| + | <ref name="lienemann2004">J. Lienemann, D. Billger, E. B. Rudnyi, A. Greiner, J. G. Korvink, "<span class="plainlinks">[http://www.nsti.org/procs/Nanotech2004v2/6/W58.01 MEMS Compact Modeling Meets Model Order Reduction: Examples of the Application of Arnoldi Methods to Microsystem Devices]</span>", TechConnect Briefs (Technical Proceedings of the 2004 NSTI Nanotechnology Conference and Trade Show, Volume 2): 303--306, 2004.</ref> |
||
| − | application of arnoldi methods formicrosystem devices," Nanotech, 2004, pp. 303–306. |
||
| + | |||
| + | <ref name="Moo07">C. Moosmann, "<span class="plainlinks">[http://www.freidok.uni-freiburg.de/volltexte/3971/ ParaMOR Model Order Reduction for parameterized MEMS applications]</span>", PhD thesis, Department of Microsystems Engineering, University of Freiburg, Freiburg, Germany 2007.</ref> |
||
| + | </references> |
||
| − | [2]C. Moosmann, ``ParaMOR---- |
||
| − | Model Order Reduction for parameterized MEMS applications," PhD thesis, Department of Microsystems Engineering, |
||
| − | University of Freiburg, 2007. |
||
| + | ==Contact== |
||
| − | [3]B. Salimbahrami, R. Eid, B. Lohmann, ``Model Reduction by Second Order |
||
| − | Krylov Subspaces: Extensions, Stability and Proportional Damping," |
||
| − | \newblock{\em IEEE International Symposium on Intelligent Control} 2006, |
||
| − | pp. 2997–3002. |
||
| + | '' [[User:Feng]] '' |
||
| − | Fig.1 |
||
| − | [[File:Gyroscope.jpg]] |
||
Latest revision as of 06:35, 17 June 2025
| Background | |
|---|---|
| Benchmark ID |
modifiedGyroscope_n17931m1q1 |
| Category |
misc |
| System-Class |
AP-LTI-SOS |
| Parameters | |
| nstates |
17931
|
| ninputs |
1 |
| noutputs |
1 |
| nparameters |
3 |
| components |
B, C, E, K, M |
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description
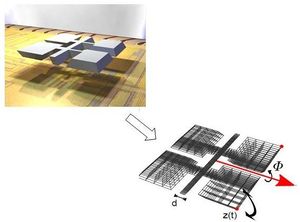
The device is a MEMS gyroscope based on the butterfly gyroscope [1] developed at the Imego institute in Gothenburg, Sweden (see also: Butterfly Gyroscope, where a non-parametrized model for the device is given). A gyroscope is a device used to measure angular rates in up to three axes.
The basic working principle of the gyroscope can be described as follows, see also [2].
Without applied external rotation, the paddles vibrate in phase with the function 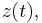 see Fig. 1.
Under the influence of an external rotation about the
see Fig. 1.
Under the influence of an external rotation about the  -axis (drawn in red),
an additional force due to the Coriolis acceleration acts upon the paddles.
This force leads to an additional small out-of-phase vibration between two paddles on the same side of the bearing.
This out-of phase vibration is measured as the difference of the
-axis (drawn in red),
an additional force due to the Coriolis acceleration acts upon the paddles.
This force leads to an additional small out-of-phase vibration between two paddles on the same side of the bearing.
This out-of phase vibration is measured as the difference of the 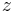 -displacement of the nodes with the red dots.
Thus, measuring the displacement of two adjacent paddles, the rotation velocity can be ascertained.
-displacement of the nodes with the red dots.
Thus, measuring the displacement of two adjacent paddles, the rotation velocity can be ascertained.
Motivation
When planning for and making decisions on future improvements of the butterfly gyroscope, it is of importance to improve the efficiency of the gyro simulations. Repeated analysis of the sensor structure have to be conducted with respect to a number of important issues. Examples of such are sensitivity to shock, linear and angular vibration sensitivity, reaction to large rates and/or acceleration, different types of excitation load cases and the effect of force-feedback. The use of model order reduction indeed decreases run time for repeated simulations.
The Parametrized Model
Two parameters are of special interest for the model.
The first one is the quantity that is to be sensed, the rotation velocity 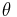 around the
around the  -axes.
The second parameter is the width of the bearing,
-axes.
The second parameter is the width of the bearing, 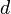 .
The parametrized system below is obtained by finite element discretization of the parametrized model (in the form of partial differential equations) for the gyroscope.
The details of constructing the parametrized system can be found in [2].
The system is of the following form:
.
The parametrized system below is obtained by finite element discretization of the parametrized model (in the form of partial differential equations) for the gyroscope.
The details of constructing the parametrized system can be found in [2].
The system is of the following form:
Here,
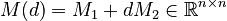 is the mass matrix,
is the mass matrix,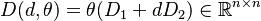 is the damping matrix,
is the damping matrix,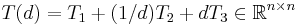 is the stiffness matrix,
is the stiffness matrix,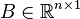 is the load vector,
is the load vector,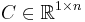 is the output matrix,
is the output matrix,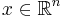 is the state vector,
is the state vector,- and
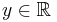 is the output response.
is the output response.
The quantity of interest 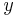 of the system is
of the system is  , which is the difference of the displacement
, which is the difference of the displacement 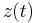 between the two red markings on the east side of the bearing (see xx--CrossReference--dft--fig:gyro--xx).
between the two red markings on the east side of the bearing (see xx--CrossReference--dft--fig:gyro--xx).
The parameters of the system, 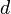 and
and 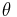 , represent the width of the bearing(
, represent the width of the bearing(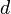 ) and the rotation velocity along the
) and the rotation velocity along the  -axis (
-axis (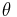 ), with the ranges:
), with the ranges: ![\theta\in [10^{-7}, 10^{-5}]](/morwiki/images/math/c/7/b/c7b0efa19e225aa5e038426cd80c3295.png) and
and ![d\in [1,2]](/morwiki/images/math/2/4/4/244c3333a4e36be25805ee4d952a245e.png) .
.
The device works in the frequency range ![f \in [0.025, 0.25]](/morwiki/images/math/8/f/1/8f1b9fd6143653e37abb4aeea17e1673.png) MHz and the degrees of freedom are
MHz and the degrees of freedom are 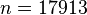 .
.
Data
The model is generated in ANSYS.
The system matrices 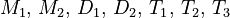 , and
, and  are in the MatrixMarket format, and can be downloaded here: Gyroscope_modi.tgz. The matrix
are in the MatrixMarket format, and can be downloaded here: Gyroscope_modi.tgz. The matrix  defines the output, which has zeros on all the entries, except on the 2315th entry, where the value is
defines the output, which has zeros on all the entries, except on the 2315th entry, where the value is 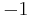 , and on the 5806th entry, the value is
, and on the 5806th entry, the value is 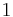 ;
in MATLAB notation, it is C(1,2315) = -1 and C(1,5806) = 1.
;
in MATLAB notation, it is C(1,2315) = -1 and C(1,5806) = 1.
The matrices have been reindexed for MORB, as shown in the next section. In particular, 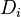 is denoted instead by
is denoted instead by 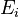 , and
, and 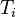 by
by 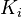 .
.
Dimensions
System structure:
System dimensions:
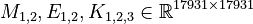 ,
,
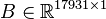 ,
,
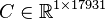 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- The MORwiki Community, Modified Gyroscope. MORwiki - Model Order Reduction Wiki, 2018. https://modelreduction.org/morwiki/Modified_Gyroscope
@MISC{morwiki_modgyro,
author = {{The MORwiki Community}},
title = {Modified Gyroscope},
howpublished = {{MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Modified_Gyroscope},
year = 2018
}
References
- ↑ J. Lienemann, D. Billger, E. B. Rudnyi, A. Greiner, J. G. Korvink, "MEMS Compact Modeling Meets Model Order Reduction: Examples of the Application of Arnoldi Methods to Microsystem Devices", TechConnect Briefs (Technical Proceedings of the 2004 NSTI Nanotechnology Conference and Trade Show, Volume 2): 303--306, 2004.
- ↑ 2.0 2.1 C. Moosmann, "ParaMOR Model Order Reduction for parameterized MEMS applications", PhD thesis, Department of Microsystems Engineering, University of Freiburg, Freiburg, Germany 2007.