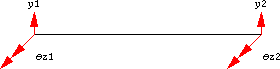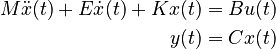(Added categories and morwiki citation, some minor changes) |
|||
| (12 intermediate revisions by 7 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
[[Category:Oberwolfach]] |
[[Category:Oberwolfach]] |
||
| Line 10: | Line 7: | ||
[[Category:SISO]] |
[[Category:SISO]] |
||
[[Category:Sparse]] |
[[Category:Sparse]] |
||
| + | |||
| + | {{Infobox |
||
| + | |Title = Linear 1D Beam |
||
| + | |Benchmark ID = |
||
| + | * linear1DBeam_n14m1q1 |
||
| + | * linear1DBeam_n18m1q1 |
||
| + | * linear1DBeam_n19994m1q1 |
||
| + | * linear1DBeam_n19998m1q1 |
||
| + | |Category = oberwolfach |
||
| + | |System-Class = LTI-SOS |
||
| + | |nstates = |
||
| + | * 14 |
||
| + | * 18 |
||
| + | * 19994 |
||
| + | * 19998 |
||
| + | |ninputs = 1 |
||
| + | |noutputs = 1 |
||
| + | |nparameters = 0 |
||
| + | |components = B, C, E, K, M |
||
| + | |License = NA |
||
| + | |Creator = [[User:Himpe]] |
||
| + | |Editor = |
||
| + | * [[User:Himpe]] |
||
| + | * [[User:Mlinaric]] |
||
| + | * [[User:Hund]] |
||
| + | |Zenodo-link = NA |
||
| + | }} |
||
| Line 18: | Line 42: | ||
<figure id="fig4">[[File:Beam4.gif|490px|thumb|right|Figure 4]]</figure> |
<figure id="fig4">[[File:Beam4.gif|490px|thumb|right|Figure 4]]</figure> |
||
| − | Moving structures are an essential part |
+ | Moving structures are an essential part of many microsystem devices, among them fluidic components like pumps and electrically controllable valves, sensing cantilevers, and optical structures. |
Several actuation principles can be employed on microscopic length scales, the most frequent certainly the electromagnetic forces. |
Several actuation principles can be employed on microscopic length scales, the most frequent certainly the electromagnetic forces. |
||
| Line 28: | Line 52: | ||
Accurate modelling of such a system typically leads to high order models. |
Accurate modelling of such a system typically leads to high order models. |
||
| − | The tasks of simulation, analysis and controller design of high order nonlinear control systems can be simplified by reducing the order of the original system and |
+ | The tasks of simulation, analysis and controller design of high order nonlinear control systems can be simplified by reducing the order of the original system and approximating it by a lower order model. |
| − | A application of electrostatic moving structures are e.g. RF switches or filters. |
+ | A application of electrostatic moving structures are e.g. [[wikipedia:RF_switch|RF switches]] or filters. |
Given a simple enough shape, they often can be modelled as one-dimensional beams embedded in two or three dimensional space. |
Given a simple enough shape, they often can be modelled as one-dimensional beams embedded in two or three dimensional space. |
||
| Line 53: | Line 77: | ||
|} |
|} |
||
| − | See |
+ | See Fig. 2 for Degree of Freedom <math>x</math>, Fig. 3 for Degree of Freedom <math>\theta_x</math> and Fig. 4 for Degrees of freedom <math>y</math> and <math>\theta_z</math>. |
The beam is supported either on the left side or on both sides. For the left side (fixed) support, |
The beam is supported either on the left side or on both sides. For the left side (fixed) support, |
||
| Line 121: | Line 145: | ||
|Compressed size [B] |
|Compressed size [B] |
||
|- |
|- |
||
| + | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Linear1dBeam-dim1e1-LF10.zip Linear1dBeam-dim1e1-LF10.zip] |
||
| − | |[https://portal.uni-freiburg.de/imteksimulation/downloads/benchmark/Linear%201D%20Beam%20%2838861%29/files/fileinnercontentproxy.2010-01-31.3349728177 LF10.zip] |
||
|flexural (<math>y</math> and <math>\theta_z</math>) |
|flexural (<math>y</math> and <math>\theta_z</math>) |
||
|10 |
|10 |
||
| Line 128: | Line 152: | ||
|2384 |
|2384 |
||
|- |
|- |
||
| + | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Linear1dBeam-dim1e4-LF10000.zip Linear1dBeam-dim1e4-LF10000.zip] |
||
| − | |[https://portal.uni-freiburg.de/imteksimulation/downloads/benchmark/Linear%201D%20Beam%20%2838861%29/files/fileinnercontentproxy.2010-01-31.3358570716 LF10000.zip] |
||
|flexural (<math>y</math> and <math>\theta_z</math>) |
|flexural (<math>y</math> and <math>\theta_z</math>) |
||
|10000 |
|10000 |
||
| Line 135: | Line 159: | ||
|716807 |
|716807 |
||
|- |
|- |
||
| + | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Linear1dBeam-dim1e1-LFAT5.zip Linear1dBeam-dim1e1-LFAT5.zip] |
||
| − | |[https://portal.uni-freiburg.de/imteksimulation/downloads/benchmark/Linear%201D%20Beam%20%2838861%29/files/fileinnercontentproxy.2010-01-31.3367011092 LFAT5.zip] |
||
|flexural (<math>y</math> and <math>\theta_z</math>), axial, torsional |
|flexural (<math>y</math> and <math>\theta_z</math>), axial, torsional |
||
|5 |
|5 |
||
| Line 142: | Line 166: | ||
|2255 |
|2255 |
||
|- |
|- |
||
| + | |[https://csc.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Linear1dBeam-dim1e5-LFAT5000.zip Linear1dBeam-dim1e5-LFAT5000.zip] |
||
| − | |[https://portal.uni-freiburg.de/imteksimulation/downloads/benchmark/Linear%201D%20Beam%20%2838861%29/files/fileinnercontentproxy.2010-01-31.3373723032 LFAT5000.zip] |
||
|flexural (<math>y</math> and <math>\theta_z</math>), axial, torsional |
|flexural (<math>y</math> and <math>\theta_z</math>), axial, torsional |
||
| + | |5000 |
||
| − | |50000 |
||
|19994 |
|19994 |
||
|5532532 |
|5532532 |
||
| Line 161: | Line 185: | ||
where <math>B</math> is a <math>n \times 1</math> matrix and <math>C</math> is a <math>1 \times n</math> matrix with the only nonzero entry at the <math>y</math> DOF of the middle node. |
where <math>B</math> is a <math>n \times 1</math> matrix and <math>C</math> is a <math>1 \times n</math> matrix with the only nonzero entry at the <math>y</math> DOF of the middle node. |
||
| − | Details of the implementation are available in a separate [https:// |
+ | Details of the implementation are available in a separate [https://www.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/Linear1dBeam.pdf report]. A typical input to this system is a step response; periodic on/off switching is also possible. |
The reduced model should thus both represent the step response as well as the possible influence of higher order harmonics. |
The reduced model should thus both represent the step response as well as the possible influence of higher order harmonics. |
||
See also <ref name="lienemann2006"/>. |
See also <ref name="lienemann2006"/>. |
||
| Line 195: | Line 219: | ||
* For the benchmark itself and its data: |
* For the benchmark itself and its data: |
||
| − | :: Oberwolfach Benchmark Collection '''Linear 1D Beam'''. hosted at MORwiki - Model Order Reduction Wiki, 2004. http://modelreduction.org/index.php/Linear_1D_Beam |
+ | :: Oberwolfach Benchmark Collection, '''Linear 1D Beam'''. hosted at MORwiki - Model Order Reduction Wiki, 2004. http://modelreduction.org/index.php/Linear_1D_Beam |
| − | + | @MISC{morwiki_linear_beam, |
|
| − | + | author = <nowiki>{{Oberwolfach Benchmark Collection}}</nowiki>, |
|
| − | + | title = {Linear 1{D} Beam}, |
|
| − | + | howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki}, |
|
| − | + | url = <nowiki>{https://modelreduction.org/morwiki/Linear_1D_Beam}</nowiki>, |
|
| − | + | year = 2004 |
|
| + | } |
||
| − | } |
||
| + | |||
| + | * For the background on the benchmark: |
||
| + | |||
| + | @TechReport{morLieRK06, |
||
| + | title = {MST MEMS Model Order Reduction: Requirements and Benchmarks}, |
||
| + | author = {J. Lienemann, E.B. Rudnyi and J.G. Korvink}, |
||
| + | journal = {Linear Algebra and its Applications}, |
||
| + | year = 2006, |
||
| + | volume = 415, |
||
| + | issue = 2--3, |
||
| + | pages = {469--498}, |
||
| + | month = {June}, |
||
| + | publisher = {Elsevier}, |
||
| + | doi = {10.1016/j.laa.2005.04.002} |
||
| + | } |
||
| + | |||
==References== |
==References== |
||
Latest revision as of 06:32, 17 June 2025
| Background | |
|---|---|
| Benchmark ID |
|
| Category |
oberwolfach |
| System-Class |
LTI-SOS |
| Parameters | |
| nstates |
|
| ninputs |
1 |
| noutputs |
1 |
| nparameters |
0 |
| components |
B, C, E, K, M |
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Description
Moving structures are an essential part of many microsystem devices, among them fluidic components like pumps and electrically controllable valves, sensing cantilevers, and optical structures.
Several actuation principles can be employed on microscopic length scales, the most frequent certainly the electromagnetic forces. While electrostatic actuation falls behind at the macro scale, the effect of charged bodies outperforms magnetic forces in the micro scale both in terms of performance and fabrication expense.
While the single component can easily be simulated on a usual desktop computer, the calculation of a system of many coupled devices still presents a challenge. This challenge is raised by the fact that many of these devices show a nonlinear behavior. Especially for electrostatic structures, a further difficulty is the large reach of the electrostatic forces, leading to a strong spatial coupling of charges.
Accurate modelling of such a system typically leads to high order models. The tasks of simulation, analysis and controller design of high order nonlinear control systems can be simplified by reducing the order of the original system and approximating it by a lower order model.
A application of electrostatic moving structures are e.g. RF switches or filters. Given a simple enough shape, they often can be modelled as one-dimensional beams embedded in two or three dimensional space.
Model Description
This model describes a slender beam with four degrees of freedom per node:

|
Axial displacement |
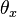
|
Axial rotation |
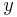
|
Flexural displacement |
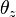
|
Flexural rotation |
See Fig. 2 for Degree of Freedom  , Fig. 3 for Degree of Freedom
, Fig. 3 for Degree of Freedom 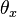 and Fig. 4 for Degrees of freedom
and Fig. 4 for Degrees of freedom 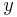 and
and 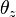 .
.
The beam is supported either on the left side or on both sides. For the left side (fixed) support,
the force is applied on the rightmost node in 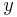 direction, whereas for the support on both sides (simply supported), a node in the middle is loaded.
The damping matrix is calculated by a linear combination of the mass matrix
direction, whereas for the support on both sides (simply supported), a node in the middle is loaded.
The damping matrix is calculated by a linear combination of the mass matrix  and the stiffness matrix
and the stiffness matrix 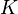 .
.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[1]; No. 38861.
Data
Based on the finite element discretization presented in[2], an interactive matrix generator has been created using Wolfram Research's webMathematica. However, models produced by this generator are in the DSIF[3] format, which allows for nonlinear terms. For the purpose of the benchmark collection, we have precomputed four systems and converted them to the Matrix market format which is easier to import in standard computer algebra packages.
All examples are made for a steel beam with the following properties:
| Property | Value |
| Beam length (l) | 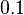 m m
|
| Material density (rho) | 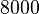 kg/m3 kg/m3
|
| Cross-sectional area (A) | 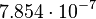 m2 m2
|
| Moment of inertia (I) |  m4 m4
|
| Polar moment of inertia (J) | 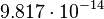
|
| Modulus of elasticity (E) | 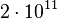 Pa Pa
|
| Poisson ratio (nu) | 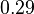
|
Contribution of  to damping to damping
|

|
Contribution of 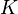 to damping to damping
|
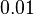
|
| Support | Simple, both sides |
The following examples are available (all files are compressed .zip archives, Units: SI):
| File | Degrees of freedom | Number of nodes | Number of equations | File size [B] | Compressed size [B] |
| Linear1dBeam-dim1e1-LF10.zip | flexural (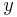 and and 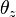 ) )
|
10 | 18 | 5935 | 2384 |
| Linear1dBeam-dim1e4-LF10000.zip | flexural (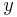 and and 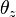 ) )
|
10000 | 19998 | 6640324 | 716807 |
| Linear1dBeam-dim1e1-LFAT5.zip | flexural (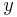 and and 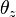 ), axial, torsional ), axial, torsional
|
5 | 14 | 4045 | 2255 |
| Linear1dBeam-dim1e5-LFAT5000.zip | flexural (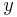 and and 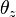 ), axial, torsional ), axial, torsional
|
5000 | 19994 | 5532532 | 627991 |
The zip files contain matrices  ,
,  ,
, 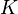 ,
,  and
and  for the following system of equations:
for the following system of equations:
where  is a
is a 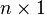 matrix and
matrix and  is a
is a 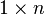 matrix with the only nonzero entry at the
matrix with the only nonzero entry at the 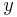 DOF of the middle node.
DOF of the middle node.
Details of the implementation are available in a separate report. A typical input to this system is a step response; periodic on/off switching is also possible. The reduced model should thus both represent the step response as well as the possible influence of higher order harmonics. See also [4].
Dimensions
System structure:
System dimensions:
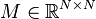 ,
,
 ,
,
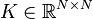 ,
,
 ,
,

System variants:
LF10:  ,
LF100:
,
LF100: 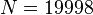 ,
LFAT5:
,
LFAT5: 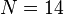 ,
LFAT5000:
,
LFAT5000: 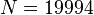 ,
,
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Oberwolfach Benchmark Collection, Linear 1D Beam. hosted at MORwiki - Model Order Reduction Wiki, 2004. http://modelreduction.org/index.php/Linear_1D_Beam
@MISC{morwiki_linear_beam,
author = {{Oberwolfach Benchmark Collection}},
title = {Linear 1{D} Beam},
howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
url = {https://modelreduction.org/morwiki/Linear_1D_Beam},
year = 2004
}
- For the background on the benchmark:
@TechReport{morLieRK06,
title = {MST MEMS Model Order Reduction: Requirements and Benchmarks},
author = {J. Lienemann, E.B. Rudnyi and J.G. Korvink},
journal = {Linear Algebra and its Applications},
year = 2006,
volume = 415,
issue = 2--3,
pages = {469--498},
month = {June},
publisher = {Elsevier},
doi = {10.1016/j.laa.2005.04.002}
}
References
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, In: Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ W. Weaver Jr., S.P. Timoshenko, D.H. Young, Vibration problems in engineering, 5th ed., Wiley, 1990.
- ↑ J. Lienemann, B. Salimbahrami, B. Lohmann, J.G. Korvink, A File Format for the Exchange of Nonlinear Dynamical ODE Systems, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 317--326, 2005.
- ↑ J. Lienemann, E.B. Rudnyi, J.G. Korvink MST MEMS model order reduction: Requirements and benchmarks, Linear Algebra and its Applications 415(2--3): 469--498, 2006.