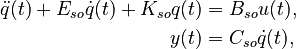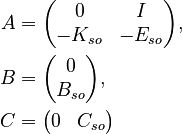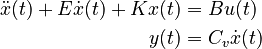(remove preliminary and stub warnings) |
(Small fix, Python code, second-order form) |
||
| Line 6: | Line 6: | ||
==Description: Motion Problem in a Building== |
==Description: Motion Problem in a Building== |
||
| − | This benchmark models the displacement of a multi- |
+ | This benchmark models the displacement of a multi-story building for example during an Earthquake. |
More details can be found in <ref name="antoulas01"/> and <ref name="chahlaoui02"/>, <ref name="chahlaoui05"/>. |
More details can be found in <ref name="antoulas01"/> and <ref name="chahlaoui02"/>, <ref name="chahlaoui05"/>. |
||
| Line 16: | Line 16: | ||
This benchmark is part of the '''SLICOT Benchmark Examples for Model Reduction'''<ref name="chahlaoui05"/>. |
This benchmark is part of the '''SLICOT Benchmark Examples for Model Reduction'''<ref name="chahlaoui05"/>. |
||
| − | |||
==Data== |
==Data== |
||
| Line 22: | Line 21: | ||
The system matrices <math>A</math>, <math>B</math>, <math>C</math> are available from the [http://slicot.org/20-site/126-benchmark-examples-for-model-reduction SLICOT benchmarks] page: [http://slicot.org/objects/software/shared/bench-data/build.zip build.zip] and are stored as MATLAB [https://www.mathworks.com/help/matlab/import_export/mat-file-versions.html .mat] file. |
The system matrices <math>A</math>, <math>B</math>, <math>C</math> are available from the [http://slicot.org/20-site/126-benchmark-examples-for-model-reduction SLICOT benchmarks] page: [http://slicot.org/objects/software/shared/bench-data/build.zip build.zip] and are stored as MATLAB [https://www.mathworks.com/help/matlab/import_export/mat-file-versions.html .mat] file. |
||
| + | Here is [https://www.python.org Python] code for loading the matrices (<math>A</math> is stored as a sparse matrix that is mostly full and <math>C</math> is stored as an array of 8-bit unsigned integers): |
||
| + | |||
| + | :<source lang="python"> |
||
| + | import numpy as np |
||
| + | from scipy.io import loadmat |
||
| + | |||
| + | mat = loadmat('build.mat') |
||
| + | A = mat['A'].toarray() |
||
| + | B = mat['B'] |
||
| + | C = mat['C'].astype(np.float_) |
||
| + | </source> |
||
| + | |||
| + | The <math>(A, B, C)</math> represents a second-order system |
||
| + | |||
| + | :<math> |
||
| + | \begin{align} |
||
| + | \ddot{q}(t) + E_{so} \dot{q}(t) + K_{so} q(t) &= B_{so} u(t), \\ |
||
| + | y(t) &= C_{so} \dot{q}(t), |
||
| + | \end{align} |
||
| + | </math> |
||
| + | |||
| + | as |
||
| + | |||
| + | :<math> |
||
| + | \begin{align} |
||
| + | A &= |
||
| + | \begin{pmatrix} |
||
| + | 0 & I \\ |
||
| + | -K_{so} & -E_{so} |
||
| + | \end{pmatrix}, \\ |
||
| + | B &= |
||
| + | \begin{pmatrix} |
||
| + | 0 \\ |
||
| + | B_{so} |
||
| + | \end{pmatrix}, \\ |
||
| + | C &= |
||
| + | \begin{pmatrix} |
||
| + | 0 & C_{so} |
||
| + | \end{pmatrix} |
||
| + | \end{align} |
||
| + | </math> |
||
| + | |||
| + | Here is [https://www.python.org Python] code for checking the structure and extracting the second-order matrices: |
||
| + | |||
| + | :<source lang="python"> |
||
| + | n = 48 |
||
| + | n2 = n // 2 |
||
| + | |||
| + | assert np.all(A[:n2, :n2] == 0) |
||
| + | assert np.all(A[:n2, n2:] == np.eye(n2)) |
||
| + | assert np.all(B[:n2] == 0) |
||
| + | assert np.all(C[:, :n2] == 0) |
||
| + | |||
| + | Eso = -A[n2:, n2:] |
||
| + | Kso = -A[n2:, :n2] |
||
| + | Bso = B[n2:] |
||
| + | Cso = C[:, n2:] |
||
| + | </source> |
||
==Dimensions== |
==Dimensions== |
||
| + | |||
| + | ===First differential order=== |
||
System structure: |
System structure: |
||
:<math> |
:<math> |
||
| − | \begin{ |
+ | \begin{align} |
| − | \dot{x}(t) &= |
+ | \dot{x}(t) &= A x(t) + B u(t) \\ |
| − | y(t) &= |
+ | y(t) &= C x(t) |
| − | \end{ |
+ | \end{align} |
</math> |
</math> |
||
| Line 40: | Line 99: | ||
<math>C \in \mathbb{R}^{1 \times 48}</math>. |
<math>C \in \mathbb{R}^{1 \times 48}</math>. |
||
| + | ===Second differential order=== |
||
| + | |||
| + | System structure: |
||
| + | |||
| + | :<math> |
||
| + | \begin{align} |
||
| + | \ddot{x}(t) + E \dot{x}(t) + K x(t) &= B u(t) \\ |
||
| + | y(t) &= C_v \dot{x}(t) |
||
| + | \end{align} |
||
| + | </math> |
||
| + | |||
| + | System dimensions: |
||
| + | |||
| + | <math>E, K \in \mathbb{R}^{24 \times 24}</math>, |
||
| + | <math>B \in \mathbb{R}^{24 \times 1}</math>, |
||
| + | <math>C_v \in \mathbb{R}^{1 \times 24}</math>. |
||
==Citation== |
==Citation== |
||
Revision as of 16:43, 29 August 2023
Description: Motion Problem in a Building
This benchmark models the displacement of a multi-story building for example during an Earthquake. More details can be found in [1] and [2], [3].
Earthquake Model
Origin
This benchmark is part of the SLICOT Benchmark Examples for Model Reduction[3].
Data
The system matrices  ,
,  ,
,  are available from the SLICOT benchmarks page: build.zip and are stored as MATLAB .mat file.
are available from the SLICOT benchmarks page: build.zip and are stored as MATLAB .mat file.
Here is Python code for loading the matrices ( is stored as a sparse matrix that is mostly full and
is stored as a sparse matrix that is mostly full and  is stored as an array of 8-bit unsigned integers):
is stored as an array of 8-bit unsigned integers):
import numpy as np from scipy.io import loadmat mat = loadmat('build.mat') A = mat['A'].toarray() B = mat['B'] C = mat['C'].astype(np.float_)
The 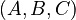 represents a second-order system
represents a second-order system
as
Here is Python code for checking the structure and extracting the second-order matrices:
n = 48 n2 = n // 2 assert np.all(A[:n2, :n2] == 0) assert np.all(A[:n2, n2:] == np.eye(n2)) assert np.all(B[:n2] == 0) assert np.all(C[:, :n2] == 0) Eso = -A[n2:, n2:] Kso = -A[n2:, :n2] Bso = B[n2:] Cso = C[:, n2:]
Dimensions
First differential order
System structure:
System dimensions:
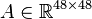 ,
,
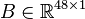 ,
,
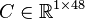 .
.
Second differential order
System structure:
System dimensions:
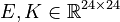 ,
,
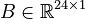 ,
,
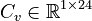 .
.
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org
@MANUAL{slicot_build,
title = {{SLICOT} - Subroutine Library in Systems and Control Theory},
organization = {Niconet e.V.}
address = {\url{http://www.slicot.org}},
key = {SLICOT}
}
- For the background on the benchmark:
@ARTICLE{morAntSG01,
author = {A.C. Antoulas, D.C. Sorensen and S. Gugercin},
title = {A survey of model reduction methods for large-scale systems},
journal = {Contemporary Mathematics},
volume = {280},
pages = {193--219},
year = {2001},
doi = {10.1090/conm/280}
}
References
- ↑ A.C. Antoulas, D.C. Sorensen and S. Gugercin. A survey of model reduction methods for large-scale systems. Contemporary Mathematics, 280: 193--219, 2001.
- ↑ Y. Chahlaoui, P. Van Dooren, A collection of Benchmark examples for model reduction of linear time invariant dynamical systems, Working Note 2002-2: 2002.
- ↑ 3.0 3.1 Y. Chahlaoui, P. Van Dooren, Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.