(Created page with "{{preliminary}} <!-- Do not remove --> ==Description== The '''Porous absorber''' benchmark models the sound pressure in a cavity excited by a single harmonic load. One side o...") |
|||
| Line 1: | Line 1: | ||
{{preliminary}} <!-- Do not remove --> |
{{preliminary}} <!-- Do not remove --> |
||
| + | |||
| + | <figure id="fig:plot1"> |
||
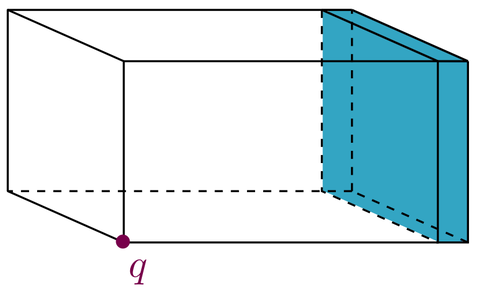
| + | [[File:Porous_absorber.png|480px|thumb|right|<caption>Sketch of the geometry. The porous material is marked in blue, the acoustic source by <math>q</math>.</caption>]] |
||
| + | </figure> |
||
| + | |||
| + | <figure id="fig:tf"> |
||
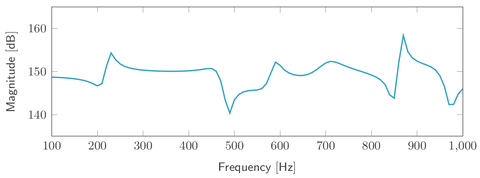
| + | [[File:Porous_absorber_frf.png|480px|thumb|right|<caption>Frequency response function.</caption>]] |
||
| + | </figure> |
||
==Description== |
==Description== |
||
Revision as of 16:01, 27 June 2023
Note: This page has not been verified by our editors.
.
Description
The Porous absorber benchmark models the sound pressure in a cavity excited by a single harmonic load. One side of the cavity is covered by a layer of poroelastic material, which adds dissipation to the system. The geometry of this model follows [1]. Various projection-based model order reduction methods have been applied and compared using this example as a benchmark in [2].
References
- ↑ R. Rumpler, P. Göransson, J.-F. Deü. "A finite element approach combining a reduced-order system, Padé approximants, and an adaptive frequency windowing for fast multi-frequency solution of poro-acoustic problems", International Journal for Numerical Methods in Engineering, 97: 759-784, 2014.
- ↑ Q. Aumann, S. W. R. Werner. "Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods", Journal of Sound and Vibration, 543: 117363, 2023.