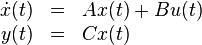m (Lund moved page FOM to Penzl's FOM: FOM is too vague and Penzl proposed this benchmark in the first place) |
(explain where FOM comes from) |
||
| Line 1: | Line 1: | ||
| − | {{preliminary}} <!-- Do not remove --> |
||
| − | |||
[[Category:benchmark]] |
[[Category:benchmark]] |
||
[[Category:SLICOT]] |
[[Category:SLICOT]] |
||
| Line 11: | Line 9: | ||
==Description== |
==Description== |
||
| − | This benchmark is an artificial example system of order <math>1006</math> from <ref name="penzl06"/> also listed in <ref name="chahlaoui02"/>. |
+ | This benchmark is an artificial example system of order <math>1006</math> from <ref name="penzl06"/> also listed in <ref name="chahlaoui02"/>. It has long been regarded as a standard "full order model" (FOM) for testing new methods. |
| + | |||
The benchmark system consists of the following system components: |
The benchmark system consists of the following system components: |
||
Revision as of 16:03, 25 August 2022
This is a stub. Please expand.
Description
This benchmark is an artificial example system of order 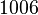 from [1] also listed in [2]. It has long been regarded as a standard "full order model" (FOM) for testing new methods.
from [1] also listed in [2]. It has long been regarded as a standard "full order model" (FOM) for testing new methods.
The benchmark system consists of the following system components:
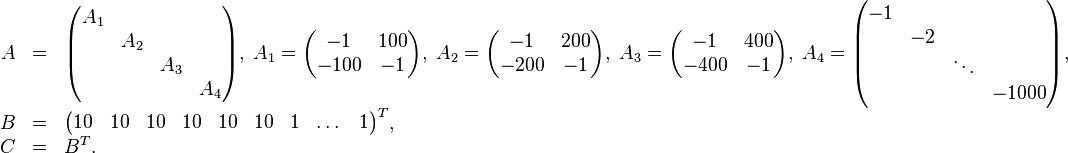
This system is a theoretical construct, but features a non-smooth Bode plot with three spikes.
MIMO Variant
In [3] a MIMO variant of this benchmark is utilized by adding random vectors to  and
and  .
.
Parametric Variant
In [4], a parametric variant of this benchmark is formulated by redefining
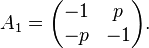
Origin
This benchmark is part of the SLICOT Benchmark Examples for Model Reduction[5].
Data
The system matrices  ,
,  ,
,  are available from the SLICOT benchmarks page: fom.zip and are stored as MATLAB .mat file.
are available from the SLICOT benchmarks page: fom.zip and are stored as MATLAB .mat file.
Dimensions
System structure:
System dimensions:
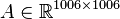 ,
,
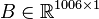 ,
,
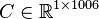 ,
,
Citation
To cite this benchmark, use the following references:
- For the benchmark itself and its data:
- Niconet e.V., SLICOT - Subroutine Library in Systems and Control Theory, http://www.slicot.org
@MANUAL{slicot_fom,
title = {{SLICOT} - Subroutine Library in Systems and Control Theory},
organization = {Niconet e.V.}
address = {\url{http://www.slicot.org}},
key = {SLICOT}
}
- For the background on the benchmark:
@ARTICLE{morPen06,
author = {T. Penzl},
title = {Algorithms for Model Reduction of Large Dynamical Systems},
journal = {Linear Algebra and its Application},
volume = {415},
number = {2--3},
pages = {322--343},
year = {2006},
doi = {10.1016/j.laa.2006.01.007}
}
References
- ↑ T. Penzl. Algorithms for Model Reduction of Large Dynamical Systems. Linear Algebra and its Application 415(2--3): 322--343, 2006.
- ↑ Y. Chahlaoui, P. Van Dooren, A collection of Benchmark examples for model reduction of linear time invariant dynamical systems, Working Note 2002-2: 2002.
- ↑ M. Heyouni, K. Jbilou, A. Messaoudi, K. Tabaa. Model Reduction in Large-Scale MIMO Dynamical Systems via the Block Lanczos Method. Computational & Applied Mathematics 27(11): 211--236, 2008.
- ↑ A. C. Ionita,A. C. Antoulas, Data-Driven Parametrized Model Reduction in the Loewner Framework, SIAM J. Sci. Comput. 36(3): A984–A1007, 2014.
- ↑ Y. Chahlaoui, P. Van Dooren, Benchmark Examples for Model Reduction of Linear Time-Invariant Dynamical Systems, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 379--392, 2005.