Bilinear PMOR method

The model reduction method we present here is applicable to linear parameter-varying (LPV) systems of the form

$\dot{x}(t)=Ax(t) + \sum_{i=1}^d p_i(t)A_i x(t)+B_0u_0(t),\quad y(t)=Cx(t),$

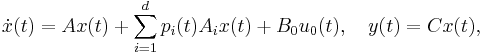
where 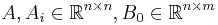$A,A_i \in \mathbb R^{n\times n}, B_0 \in \mathbb R^{n\times m}$ and $C \in \mathbb R^{p\times n}.$

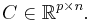
The main idea is that the structure of the above type of systems is quite similar to so-called bilinear control systems. Although belonging to the class of nonlinear control systems, the latter exhibit many features of linear time-invariant systems. In more detail, a bilinear control system is given as follows

$\dot{x}(t)=Ax(t) + \sum_{i=1}^m N_i x(t) u_i(t) + B u(t),$

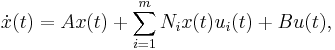
where 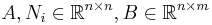$A,N_i \in \mathbb R^{n\times n}, B \in \mathbb R^{n\times m}$ and $C \in \mathbb R^{p\times n}.$

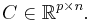
As one can see, there seems to be a close connection between LPV and bilinear systems which may be advantageous. To be more precise, following [2], we can interpret LPV systems as special bilinear system by simply setting

$\tilde{A}=A,\;\; \tilde{N}_i=0,\;\;i=1,\dots,m,\;\; \tilde{N}_i=A_i,\;\; i=m+1,\dots,m+d, \;\; \tilde{B}=\begin{bmatrix} B_0 & 0\end{bmatrix},\;\; \tilde{C}=C, \;\; \tilde{u}=\begin{bmatrix} u_0 \\ p_1(t) \\ \vdots \\ p_d(t)\end{bmatrix} .$

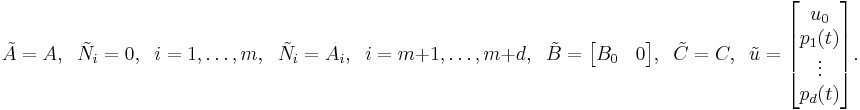
It is important to note that in this way the parameter dependency has been hidden in the structure of a bilinear system and if we use a bilinear model reduction method, we automatically end up with a structure-preserving model reduction method for LPV systems as well. Due to the above mentioned similarity of bilinear and linear control systems, one can generalize some useful and well-known linear concepts. For example, it is possible to extend the method of balanced truncation for bilinear systems. Here, we have to solve generalized Lyapunov equations of the form

$AX+XA^T +\sum_{i=1}^m N_i X N_i^T + BB^T = 0, \qquad A^TY+YA +\sum_{i=1}^m N_i^T Y N_i + C^TC = 0.$

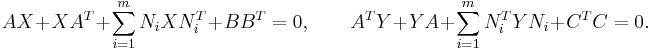
For a detailed analysis of this approach, we refer to e.g. [3]. Another possibility is to aim at a model reduction method which is optimal with respect to a certain system norm. In [1], the authors investigate a possible extension of the linear 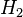$H_2$-norm and propose an algorithm which extends the well-known iterative rational Krylov algorithm (IRKA) to the bilinear setting specified above.

Both methods have been tested on several LPV control systems and seem to be a reasonable alternative to existing parametric model reduction methods.

References

[1] P. Benner and T. Breiten, Interpolation-based H2-model reduction of bilinear control systems, 2011, Preprint MPIMD/11-02.

[2] P. Benner and T. Breiten, On H2-model reduction of linear parameter-varying systems, In Proceedings in Applied Mathematics and Mechanics. Wiley InterScience, 2011.

[3] P. Benner and T. Damm, Lyapunov Equations, Energy Functionals, and Model Order Reduction of Bilinear and Stochastic Systems, SIAM J. Cont. Optim., 49 (2011), pp. 686-711.