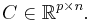(Created page with 'test') |
|||
| Line 1: | Line 1: | ||
| + | The model reduction method we present here is applicable to linear parameter-varying (LPV) systems of the form |
||
| − | test |
||
| + | |||
| + | <center> |
||
| + | <math> |
||
| + | \dot{x}(t)=Ax(t) + \sum_{i=1}^d p_i(t)A_i x(t)+B_0u_0(t),\quad y(t)=Cx(t), |
||
| + | </math> |
||
| + | </center> |
||
| + | |||
| + | where |
||
| + | <math> |
||
| + | A,A_i \in \mathbb R^{n\times n}, B_0 \in \mathbb R^{n\times m} |
||
| + | </math> |
||
| + | and |
||
| + | <math> C \in \mathbb R^{p\times n}. |
||
| + | </math> |
||
| + | |||
| + | The main idea is that the structure of the above type of systems is quite similar to so-called bilinear control systems. Although belonging to the class of nonlinear control systems, the latter exhibit many features of linear time-invariant systems. In more detail, a bilinear control system is given as follows |
||
| + | |||
| + | <center> |
||
| + | <math> |
||
| + | \dot{x}(t)=Ax(t) + \sum_{i=1}^m N_i x(t) u_i(t) + B u(t), |
||
| + | </math> |
||
| + | </center> |
||
| + | |||
| + | where |
||
| + | <math> |
||
| + | A,N \in \mathbb R^{n\times n}, B \in \mathbb R^{n\times m} |
||
| + | </math> |
||
| + | and |
||
| + | <math> C \in \mathbb R^{p\times n}. |
||
| + | </math> |
||
Revision as of 08:02, 6 December 2011
The model reduction method we present here is applicable to linear parameter-varying (LPV) systems of the form
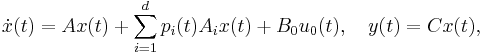
where
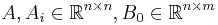 and
and
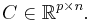
The main idea is that the structure of the above type of systems is quite similar to so-called bilinear control systems. Although belonging to the class of nonlinear control systems, the latter exhibit many features of linear time-invariant systems. In more detail, a bilinear control system is given as follows
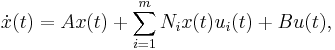
where
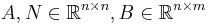 and
and