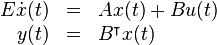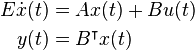(Update benchmark data file links) |
|||
| Line 33: | Line 33: | ||
</math> |
</math> |
||
| − | and can be downloaded as [https:// |
+ | and can be downloaded as [https://www.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/PeekInductor-dim1e3-spiral_inductor_peec.tar.gz PeekInductor-dim1e3-spiral_inductor_peec.tar.gz] (10.5 MB). |
Short [[wikipedia:MATLAB|Matlab]] files to: |
Short [[wikipedia:MATLAB|Matlab]] files to: |
||
| Line 41: | Line 41: | ||
* produce symmetrized standard state-space system: <math>\dot{x}(t) = A_{symm}x(t)+ B_{symm}u(t)</math>, <math>y(t) = B_{symm}^\intercal x(t)</math>, where <math>A_{symm}</math> is symmetric. |
* produce symmetrized standard state-space system: <math>\dot{x}(t) = A_{symm}x(t)+ B_{symm}u(t)</math>, <math>y(t) = B_{symm}^\intercal x(t)</math>, where <math>A_{symm}</math> is symmetric. |
||
| − | can be found in [https:// |
+ | can be found in [https://www.mpi-magdeburg.mpg.de/mpcsc/MORWIKI/Oberwolfach/PeekInductor-plot_spiral.tar.gz PeekInductor-plot_spiral.tar.gz] |
==Dimensions== |
==Dimensions== |
||
| Line 66: | Line 66: | ||
<ref name="korvink2005"> J.G. Korvink, E.B. Rudnyi, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_11 Oberwolfach Benchmark Collection]</span>, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.</ref> |
<ref name="korvink2005"> J.G. Korvink, E.B. Rudnyi, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_11 Oberwolfach Benchmark Collection]</span>, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.</ref> |
||
| − | <ref name="li2005">J.R. Li, M. Kamon, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909- |
+ | <ref name="li2005">J.R. Li, M. Kamon, <span class="plainlinks">[https://doi.org/10.1007/3-540-27909-1_23 PEEC Model of a Spiral Inductor Generated by Fasthenry]</span>. In: Dimension Reduction of Large-Scale Systems. Lecture Notes in Computational Science and Engineering, vol 45: 373--377, 2005.</ref> |
</references> |
</references> |
||
Revision as of 11:45, 17 July 2018
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
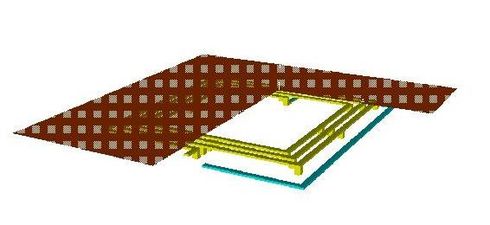
Description: Spiral Inductor PEEC Model
The description of the PEEC model of a spiral inductor can be found in LiKamon.pdf.
The complex impedance is:
A plots of 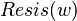 can be found in Rspiral_skin.pdf and a plot of
can be found in Rspiral_skin.pdf and a plot of 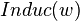 in Lspiral_skin.pdf.
in Lspiral_skin.pdf.
Origin
This benchmark is part of the Oberwolfach Benchmark Collection[1]; No. 38891, see [2].
Data
The model is of order 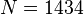 and of the form:
and of the form:
and can be downloaded as PeekInductor-dim1e3-spiral_inductor_peec.tar.gz (10.5 MB).
Short Matlab files to:
- plot
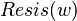 and
and 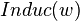 ,
, - perform a PRIMA reduction of order 50,
- produce symmetrized standard state-space system:
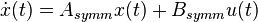 ,
, 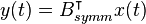 , where
, where 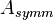 is symmetric.
is symmetric.
can be found in PeekInductor-plot_spiral.tar.gz
Dimensions
System structure:
System dimensions:
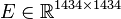 ,
,
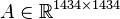 ,
,
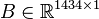 .
.
References
- ↑ J.G. Korvink, E.B. Rudnyi, Oberwolfach Benchmark Collection, Dimension Reduction of Large-Scale Systems, Lecture Notes in Computational Science and Engineering, vol 45: 311--315, 2005.
- ↑ J.R. Li, M. Kamon, PEEC Model of a Spiral Inductor Generated by Fasthenry. In: Dimension Reduction of Large-Scale Systems. Lecture Notes in Computational Science and Engineering, vol 45: 373--377, 2005.