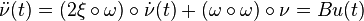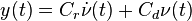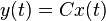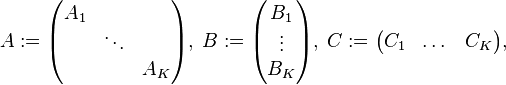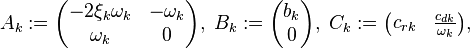m (→Data: Minor fixes) |
m (typo fix) |
||
| Line 39: | Line 39: | ||
For this benchmark the system matrix is block diagonal and thus chosen to be sparse. |
For this benchmark the system matrix is block diagonal and thus chosen to be sparse. |
||
| − | The parameters <math>\xi</math> and math>\omega</math> are sampled from a uniform random distributions <math>\mathcal{U}_{[0,\frac{1}{1000}]}^K</math> and <math>\mathcal{U}_{[0,100]}^K</math> respectively. |
+ | The parameters <math>\xi</math> and <math>\omega</math> are sampled from a uniform random distributions <math>\mathcal{U}_{[0,\frac{1}{1000}]}^K</math> and <math>\mathcal{U}_{[0,100]}^K</math> respectively. |
The components of the input matrix <math>b_k</math> are sampled form a uniform random distribution <math>\mathcal{U}_{[0,1]}</math>, |
The components of the input matrix <math>b_k</math> are sampled form a uniform random distribution <math>\mathcal{U}_{[0,1]}</math>, |
||
while the output matrix <math>C</math> is sampled from a uniform random distribution <math>\mathcal{U}_{[0,10]}</math> completely w.l.o.g, since if the components of <math>C_d</math> are random their scaling can be ignored. |
while the output matrix <math>C</math> is sampled from a uniform random distribution <math>\mathcal{U}_{[0,10]}</math> completely w.l.o.g, since if the components of <math>C_d</math> are random their scaling can be ignored. |
||
Revision as of 09:48, 2 June 2017
 Note: This page has not been verified by our editors.
Note: This page has not been verified by our editors.
Description
The flexible space structure benchmark[1] is a procedural modal model which represents structural dynamics with a selectable number actuators and sensors. This model is used for truss structures in space environments i.e. the COFS-1 (Control of Flexible Structures) mast flight experiment.
Model
In modal form the flexible space structure model for 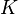 modes,
modes,  actuators and
actuators and  sensors is of second order and given by:
sensors is of second order and given by:
with the parameters 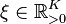 (damping ratio),
(damping ratio), 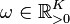 (natural frequency) and using the Hadamard product
(natural frequency) and using the Hadamard product  .
The first order representation follows for
.
The first order representation follows for 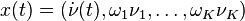 by:
by:
with the matrices:
and their components:
where 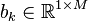 and
and 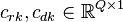 .
.
Benchmark Specifics
For this benchmark the system matrix is block diagonal and thus chosen to be sparse.
The parameters 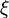 and
and  are sampled from a uniform random distributions
are sampled from a uniform random distributions ![\mathcal{U}_{[0,\frac{1}{1000}]}^K](/morwiki/images/math/2/4/b/24b74811b308c537765802cb07a302f7.png) and
and ![\mathcal{U}_{[0,100]}^K](/morwiki/images/math/3/4/2/342f256255fdd3d862d8d938a73b7d07.png) respectively.
The components of the input matrix
respectively.
The components of the input matrix 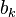 are sampled form a uniform random distribution
are sampled form a uniform random distribution ![\mathcal{U}_{[0,1]}](/morwiki/images/math/8/9/1/8914ff20760d02f585b13a7a84bf17e7.png) ,
while the output matrix
,
while the output matrix  is sampled from a uniform random distribution
is sampled from a uniform random distribution ![\mathcal{U}_{[0,10]}](/morwiki/images/math/9/e/7/9e7fb3f2b81367f97ff7a31de6e468bb.png) completely w.l.o.g, since if the components of
completely w.l.o.g, since if the components of 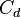 are random their scaling can be ignored.
are random their scaling can be ignored.
Data
The following Matlab code assembles the above described  ,
,  and
and  matrix for a given number of modes
matrix for a given number of modes 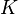 , actuators (inputs)
, actuators (inputs)  and sensors (outputs)
and sensors (outputs)  .
.
function [A,B,C] = fss(K,M,Q)
rand('seed',1009);
xi = rand(1,K)*0.001; % Sample damping ratio
omega = rand(1,K)*100.0; % Sample natural frequencies
A_k = cellfun(@(p) sparse([-2.0*p(1)*p(2),-p(2);p(2),0]), ...
num2cell([xi;omega],1),'UniformOutput',0);
A = blkdiag(A_k{:});
B = kron(rand(K,M),[1;0]);
C = 10.0*rand(Q,2*K);
end
Reference
- ↑ W. Gawronski and T. Williams, "Model Reduction for Flexible Space Structures", Journal of Guidance 14(1): 68--76, 1991