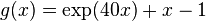m (added SISO category) |
(→Data: Fixes based on comments by Maria) |
||
| Line 54: | Line 54: | ||
==Data== |
==Data== |
||
| − | A sample MATLAB implementation is given by: |
+ | A sample procedural MATLAB implementation of order N is given by: |
<div class="thumbinner" style="width:540px;text-align:left;"> |
<div class="thumbinner" style="width:540px;text-align:left;"> |
||
<source lang="matlab"> |
<source lang="matlab"> |
||
| + | %% Procedural generation of "Nonlinear RC Ladder" benchmark system |
||
| ⚫ | |||
| + | % nonlinearity |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| − | + | A0 = sparse(N,N); |
|
| − | + | A0(1,1) = 1; |
|
| ⚫ | |||
| + | A1(1,1) = 0; |
||
| + | |||
| ⚫ | |||
| + | |||
| + | % input matrix |
||
| + | B = sparse(N,1); |
||
| + | B(1,1) = 1; |
||
| + | |||
| + | % output matrix |
||
| + | C = sparse(1,N); |
||
| + | C(1,1) = 1; |
||
| + | |||
| + | % vector field and output functional |
||
| + | xdot = @(x) -g(A0*x) + g(A1*x) - g(A2*x) + B*u; |
||
| + | y = @(x) C*x; |
||
</source> |
</source> |
||
</div> |
</div> |
||
Revision as of 09:27, 7 April 2017
Description
The nonlinear RC-ladder is an electronic test circuit introduced in[1][2]. This nonlinear first-order system models a resistor-capacitor network that exhibits a distinct nonlinear behaviour caused by the nonlinear resistors consisting of a parallel connected resistor with a diode.
Model
The underlying model is given by a (SISO) gradient system of the form[3]:
where the nonlinearity 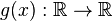 is given by:
is given by:
Input
As external input several alternatives are presented in[4], which are listed next. A simple step function is given by:
an exponential decaying input is provided by:
Additional input sources are given by conjunction of sine waves with different periods:
Data
A sample procedural MATLAB implementation of order N is given by:
%% Procedural generation of "Nonlinear RC Ladder" benchmark system
% nonlinearity
g = @(x) exp(40.0*x) + x - 1.0;
A0 = sparse(N,N);
A0(1,1) = 1;
A1 = spdiags(ones(N-1,1),-1,N,N) - speye(N);
A1(1,1) = 0;
A2 = spdiags([ones(N-1,1);0],0,N,N) - spdiags(ones(N,1),1,N,N);
% input matrix
B = sparse(N,1);
B(1,1) = 1;
% output matrix
C = sparse(1,N);
C(1,1) = 1;
% vector field and output functional
xdot = @(x) -g(A0*x) + g(A1*x) - g(A2*x) + B*u;
y = @(x) C*x;
References
- ↑ Y. Chen, "Model Reduction for Nonlinear Systems", Master Thesis, 1999.
- ↑ Y. Chen and J. White, "A quadratic method for nonlinear model order reduction", Int. conference on modelling and simulation of Microsystems semiconductors, sensors and actuators, 2000.
- ↑ M. Condon and R. Ivanov, "Empirical balanced truncation for nonlinear systems", Journal of Nonlinear Science 14(5):405--414, 2004.
- ↑ M. Condon and R. Ivanov, "Model Reduction of Nonlinear Systems", COMPEL 23(2): 547--557, 2004