Kuerschner (talk | contribs) |
Kuerschner (talk | contribs) |
||
| Line 22: | Line 22: | ||
</math> |
</math> |
||
| − | They are different ways to select this typically small subset of eigenvalues. An often used criterion is to take the eigenvalue closest to the imaginary axis, i.e. the ones with the smallest real part, and their associated eigenvectors into account. Dominant pole based modal truncation selects <math>(\lambda_i,x_i,y_i)</math> with respect to their contribution in the transfer function and is described below. |
+ | They are different ways to select this typically small subset of eigenvalues. An often used criterion is to take the eigenvalue closest to the imaginary axis, i.e. the ones with the smallest real part, and their associated eigenvectors into account. Dominant pole based modal truncation selects <math>(\lambda_i,x_i,y_i)</math> with respect to their contribution in the transfer function and is described below. |
| + | |||
| + | One advantage of such eigenvalue based MOR methods is that they can be easily adapted to more general time invariant systems, for instance, systems in second order form |
||
| + | |||
| + | <math> |
||
| + | M\ddot{x}(t)+D\dot{x}(t)+K x(t)=B u(t), \quad |
||
| + | y(t)=C_px(t)+C_v\dot x(t)+Du(t) \quad \quad (2) |
||
| + | </math> |
||
| + | |||
| + | which occur frequently in vibration analysis for mechanical systems. There, <math>M,D,K</math> being referred to as Mass, Damping, and Stiffness matrix are represent a finite element discretization of the mechanical system. In fact, a large variety of modal truncation type approaches originated in this application<ref>P. Koutsovasilis and M. Beitelschmidt, "Comparison of Model Reduction Techniques for Large Mechanical Systems", Multibody |
||
| + | System Dynamics, vol.20, no.2, pp.111,128, 2008</ref>, e.g., Condensation (Guyan reduction)<ref>R.J. Guyan, "Reduction of Stiffness and Mass Matrices", AIAA Journal, vol.3, no.2, pp.380, 1965</ref> and Component Mode Synthesis (Craig-Bampton)<ref>R. Craig and M. Bampton, "Coupling of Substructures for Dynamic Analyses", AIAA Journal, vol.6, no.7, pp.1313,1319, 1968</ref>. |
||
| + | |||
| + | ==References== |
||
| + | |||
| + | <references/> |
||
Revision as of 12:10, 24 April 2013
Description
Model truncation is one of the oldest MOR methods for linear time invariant systems
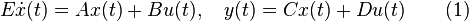
The main idea is to construct the projection matrices as ![V=[x_1,\ldots,x_r], W=[y_1,\ldots,y_r]](/morwiki/images/math/0/e/e/0ee65b7c5e9ab333049a1b288dac26d0.png) where the
where the 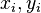 are right and left eigenvectors corresponding to
certain eigenvalues
are right and left eigenvectors corresponding to
certain eigenvalues 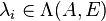 . The eigentriples
. The eigentriples 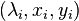 satisfy.
satisfy.
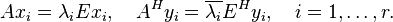
They are different ways to select this typically small subset of eigenvalues. An often used criterion is to take the eigenvalue closest to the imaginary axis, i.e. the ones with the smallest real part, and their associated eigenvectors into account. Dominant pole based modal truncation selects 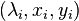 with respect to their contribution in the transfer function and is described below.
with respect to their contribution in the transfer function and is described below.
One advantage of such eigenvalue based MOR methods is that they can be easily adapted to more general time invariant systems, for instance, systems in second order form
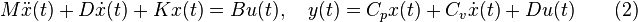
which occur frequently in vibration analysis for mechanical systems. There, 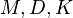 being referred to as Mass, Damping, and Stiffness matrix are represent a finite element discretization of the mechanical system. In fact, a large variety of modal truncation type approaches originated in this application[1], e.g., Condensation (Guyan reduction)[2] and Component Mode Synthesis (Craig-Bampton)[3].
being referred to as Mass, Damping, and Stiffness matrix are represent a finite element discretization of the mechanical system. In fact, a large variety of modal truncation type approaches originated in this application[1], e.g., Condensation (Guyan reduction)[2] and Component Mode Synthesis (Craig-Bampton)[3].
References
- ↑ P. Koutsovasilis and M. Beitelschmidt, "Comparison of Model Reduction Techniques for Large Mechanical Systems", Multibody System Dynamics, vol.20, no.2, pp.111,128, 2008
- ↑ R.J. Guyan, "Reduction of Stiffness and Mass Matrices", AIAA Journal, vol.3, no.2, pp.380, 1965
- ↑ R. Craig and M. Bampton, "Coupling of Substructures for Dynamic Analyses", AIAA Journal, vol.6, no.7, pp.1313,1319, 1968
