| Line 42: | Line 42: | ||
The numerical values for the different variables and <math> i = 1,\ldots,k </math> are |
The numerical values for the different variables and <math> i = 1,\ldots,k </math> are |
||
| − | * |
+ | * <math> r_i </math> equally spaced in <math>[10^{-3}, 1]</math>, with <math> r_1 = 1 </math> and <math> r_k = 10^{-3} </math>. |
| − | * <math>a_i </math> |
+ | * <math>a_i </math> equally spaced in <math> [10^{-1}, 10^3]</math>, |
| − | * <math>b_i </math> |
+ | * <math>b_i </math> equally spaced in <math>[10, 10^3]</math>, |
* <math>\varepsilon \in [1,20]</math>. |
* <math>\varepsilon \in [1,20]</math>. |
||
Revision as of 14:12, 28 November 2011
Introduction
On this page you will find a purely synthetic parametric model. The goal is to have a simple parametric model which one can use to experiment with different system orders, parameter values etc.
System description
The parameter  scales the real part of the system poles, that is,
scales the real part of the system poles, that is, 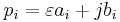 .
For a system in pole-residue form
.
For a system in pole-residue form
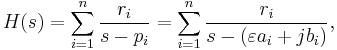
we can then write down the state-space realisation
![\widehat{A} = \varepsilon \left[\begin{array}{ccc} a_1 & & \\ & \ddots & \\ & & a_n\end{array}\right] +\left[\begin{array}{ccc} jb_1 & & \\ & \ddots & \\ & & jb_n\end{array}\right] = \varepsilon \widehat{A}_\varepsilon + \widehat{A}_0,](/morwiki/images/math/1/0/8/10836c8d14a066efc2687e4804a23487.png)
![\widehat{B} = [1,\ldots,1]^T,\quad \widehat{C} = [r_1,\ldots,r_n],\quad D = 0.](/morwiki/images/math/0/1/9/01952f4b905489c1f4686227dc13e409.png)
Notice that the system matrices have complex entries.
For simplicity, assume that  is even,
is even, 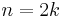 , and that all system poles are complex and ordered in complex conjugate pairs, i.e.
, and that all system poles are complex and ordered in complex conjugate pairs, i.e.
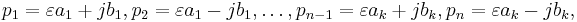
which also implies that the residues form complex conjugate pairs 
Then a realization with matrices having real entries is given by
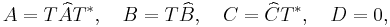
with ![T = \left[\begin{array}{ccc} T_0 & & \\ & \ddots & \\ & & T_0 \end{array}\right]](/morwiki/images/math/d/c/3/dc37eb655d2a4067275e0bda69bd1dba.png) ,
for
,
for ![T_0 = \frac{1}{\sqrt{2}}\left[\begin{array}{cc} 1 & -j\\ 1 & j \end{array}\right]](/morwiki/images/math/8/5/e/85e1ad121c593170f5387aaed11595c6.png) .
.
Numerical values
The numerical values for the different variables and 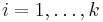 are
are
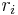 equally spaced in
equally spaced in ![[10^{-3}, 1]](/morwiki/images/math/4/f/0/4f0745565a5a24ee152ae45bfa8cb163.png) , with
, with 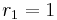 and
and 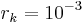 .
.
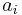 equally spaced in
equally spaced in ![[10^{-1}, 10^3]](/morwiki/images/math/c/f/d/cfd6518b053d9e1170559d2d042bcd11.png) ,
,
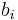 equally spaced in
equally spaced in ![[10, 10^3]](/morwiki/images/math/0/b/e/0be1e9dea133f5e55f228e67a2ea56b4.png) ,
,
![\varepsilon \in [1,20]](/morwiki/images/math/4/7/0/4700f54fb1cdd55401e73e62c64e4c0a.png) .
.
In MATLAB this is easily done as follows
test
