(some restructuring) |
m |
||
| Line 14: | Line 14: | ||
<math> y = Cx + Du</math> |
<math> y = Cx + Du</math> |
||
| − | is called balanced<ref>B.C. Moore, "<span class=" |
+ | is called balanced<ref>B.C. Moore, "<span class="plainlinks">[http://dx.doi.org/10.1109/TAC.1981.1102568 Principal component analysis in linear systems: Controllability, observability, and model reduction]</span>", IEEE Transactions on Automatic Control , vol.26, no.1, pp.17,32, Feb 1981</ref>, if the systems [[wikipedia:Controllability_Gramian|Controllability Gramian]] and [[wikipedia:Observability_Gramian|Observability Gramian]], the solutions <math>W_C</math> and <math>W_O</math> of the Lyapunov equations |
<math> AW_C+W_CA^T=-BB^T </math> |
<math> AW_C+W_CA^T=-BB^T </math> |
||
| Line 36: | Line 36: | ||
== Implementation: SR Method== |
== Implementation: SR Method== |
||
| − | The necessary balancing transformation can be computed by the SR Method<ref>A.J. Laub; M.T. Heath; C. Paige; R. Ward, "<span class=" |
+ | The necessary balancing transformation can be computed by the SR Method<ref>A.J. Laub; M.T. Heath; C. Paige; R. Ward, "<span class="plainlinks">[http://dx.doi.org/10.1109/TAC.1987.1104549 Computation of system balancing transformations and other applications of simultaneous diagonalization algorithms]</span>," IEEE Transactions on Automatic Control, vol.32, no.2, pp.115,122, Feb 1987</ref>. |
First, the Cholesky factors of the gramians <math>W_C=S^TS,\; W_O=R^TR</math> are computed. |
First, the Cholesky factors of the gramians <math>W_C=S^TS,\; W_O=R^TR</math> are computed. |
||
Next, the Singular Value Decomposition of <math> SR^T\;</math> is computed: |
Next, the Singular Value Decomposition of <math> SR^T\;</math> is computed: |
||
| Line 52: | Line 52: | ||
<math> Q= S^T U_1 \Sigma_1^{-\frac{1}{2}}.</math> |
<math> Q= S^T U_1 \Sigma_1^{-\frac{1}{2}}.</math> |
||
| − | <math>Q^TP=I_r</math> makes <math> QP^T</math> an oblique projector and hence '''Balanced Trunctation''' a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by <math>\sigma_1,\dots,\sigma_r</math>, where r is the order of the reduced system. It is possible to choose <math>r</math> via the computable error bound<ref>D.F. Enns, "<span class=" |
+ | <math>Q^TP=I_r</math> makes <math> QP^T</math> an oblique projector and hence '''Balanced Trunctation''' a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by <math>\sigma_1,\dots,\sigma_r</math>, where r is the order of the reduced system. It is possible to choose <math>r</math> via the computable error bound<ref>D.F. Enns, "<span class="plainlinks">[http://dx.doi.org/10.1109/CDC.1984.272286 Model reduction with balanced realizations: An error bound and a frequency weighted generalization]</span>," The 23rd IEEE Conference on Decision and Control, vol.23, pp.127,132, Dec. 1984</ref>: |
<math> \|\Sigma-\hat{\Sigma}\|_2 \leq 2 \|u\|_2 \sum_{k=r+1}^n\sigma_k. </math> |
<math> \|\Sigma-\hat{\Sigma}\|_2 \leq 2 \|u\|_2 \sum_{k=r+1}^n\sigma_k. </math> |
||
Revision as of 11:05, 23 April 2013
Balanced Truncation is an important projection model reduction method which delivers high quality reduced models by making an extra effort in choosing the projection subspaces.
Derivation
A stable minimal (controllable and observable) system 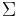 , realized by
, realized by 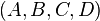
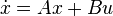
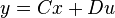
is called balanced[1], if the systems Controllability Gramian and Observability Gramian, the solutions 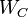 and
and 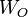 of the Lyapunov equations
of the Lyapunov equations
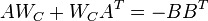
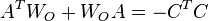
respectively, satisfy 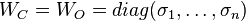 with
with  .
Since in general, the spectrum of
.
Since in general, the spectrum of 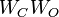 are the squared Hankel Singular Values for such a balanced system, they are given by:
are the squared Hankel Singular Values for such a balanced system, they are given by: 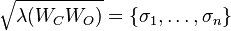 .
.
An arbitrary system 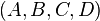 can be transformed into a balanced system
can be transformed into a balanced system 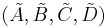 via a state-space transformation:
via a state-space transformation:
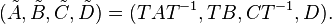
This transformed system has balanced Gramians 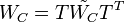 and
and 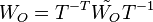 which are equal and diagonal.
The balanced systems states are ordered (descendingly) by how controllable and observable they are, thus allowing a partion of the form:
which are equal and diagonal.
The balanced systems states are ordered (descendingly) by how controllable and observable they are, thus allowing a partion of the form:
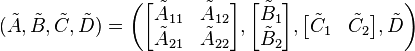 .
.
By truncating the discardable states, the truncated reduced system is then given by 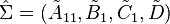 .
.
Implementation: SR Method
The necessary balancing transformation can be computed by the SR Method[2].
First, the Cholesky factors of the gramians 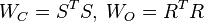 are computed.
Next, the Singular Value Decomposition of
are computed.
Next, the Singular Value Decomposition of 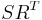 is computed:
is computed:
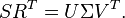
Now, partitioning 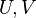 , for example based on the Hankel singuar Values, gives
, for example based on the Hankel singuar Values, gives
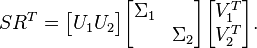
The truncation of discardable partitions 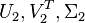 results in the reduced order model
results in the reduced order model 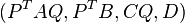 where
where
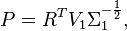
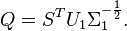
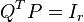 makes
makes 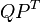 an oblique projector and hence Balanced Trunctation a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by
an oblique projector and hence Balanced Trunctation a Petrov-Galerkin projection method. The reduced model is stable with Hankel Singular Values given by  , where r is the order of the reduced system. It is possible to choose
, where r is the order of the reduced system. It is possible to choose  via the computable error bound[3]:
via the computable error bound[3]:
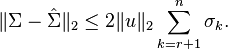
References
- ↑ B.C. Moore, "Principal component analysis in linear systems: Controllability, observability, and model reduction", IEEE Transactions on Automatic Control , vol.26, no.1, pp.17,32, Feb 1981
- ↑ A.J. Laub; M.T. Heath; C. Paige; R. Ward, "Computation of system balancing transformations and other applications of simultaneous diagonalization algorithms," IEEE Transactions on Automatic Control, vol.32, no.2, pp.115,122, Feb 1987
- ↑ D.F. Enns, "Model reduction with balanced realizations: An error bound and a frequency weighted generalization," The 23rd IEEE Conference on Decision and Control, vol.23, pp.127,132, Dec. 1984
