| Line 5: | Line 5: | ||
== System description == |
== System description == |
||
| − | The parameter <math>\varepsilon</math> scales the real part of the system poles, that is, <math> |
+ | The parameter <math>\varepsilon</math> scales the real part of the system poles, that is, <math>p_i=\varepsilon a_i+jb_i</math>. |
| − | + | For a system in pole-residue form |
|
| + | |||
<math> H(s) = \sum_{i=1}^{n}\frac{r_i}{s-p_i} = \sum_{i=1}^{n}\frac{r_i}{s-(\varepsilon a_i+jb_i)} ,</math> |
<math> H(s) = \sum_{i=1}^{n}\frac{r_i}{s-p_i} = \sum_{i=1}^{n}\frac{r_i}{s-(\varepsilon a_i+jb_i)} ,</math> |
||
| + | |||
| − | + | we can then write down the state-space realisation |
|
| + | |||
<math>\widehat{A} = \varepsilon \left[\begin{array}{ccc} a_1 & & \\ & \ddots & \\ & & a_n\end{array}\right] +\left[\begin{array}{ccc} jb_1 & & \\ & \ddots & \\ & & jb_n\end{array}\right] = \varepsilon \widehat{A}_\varepsilon + \widehat{A}_0,</math> |
<math>\widehat{A} = \varepsilon \left[\begin{array}{ccc} a_1 & & \\ & \ddots & \\ & & a_n\end{array}\right] +\left[\begin{array}{ccc} jb_1 & & \\ & \ddots & \\ & & jb_n\end{array}\right] = \varepsilon \widehat{A}_\varepsilon + \widehat{A}_0,</math> |
||
<math>\widehat{B} = [1,\ldots,1]^T,\quad \widehat{C} = [r_1,\ldots,r_n],\quad D = 0.</math> |
<math>\widehat{B} = [1,\ldots,1]^T,\quad \widehat{C} = [r_1,\ldots,r_n],\quad D = 0.</math> |
||
| + | |||
| + | |||
Notice that the system matrices have complex entries. |
Notice that the system matrices have complex entries. |
||
| Line 20: | Line 25: | ||
For simplicity, assume that <math> n </math> is even, <math> n=2k </math>, and that all system poles are complex and ordered in complex conjugate pairs, i.e. |
For simplicity, assume that <math> n </math> is even, <math> n=2k </math>, and that all system poles are complex and ordered in complex conjugate pairs, i.e. |
||
| − | <math> p_1 = \varepsilon a_1+jb_1, p_2 = \varepsilon a_1-jb_1, \ldots, p_{n-1} = \varepsilon a_k+jb_k, p_n = \varepsilon a_k-jb_k |
+ | <math> p_1 = \varepsilon a_1+jb_1, p_2 = \varepsilon a_1-jb_1, \ldots, p_{n-1} = \varepsilon a_k+jb_k, p_n = \varepsilon a_k-jb_k, </math> |
| − | + | which also implies that the residues form complex conjugate pairs <math>r_1, \bar{r}_1,\ldots , r_k, \bar{r}_k.</math> |
|
Then a realization with matrices having real entries is given by |
Then a realization with matrices having real entries is given by |
||
| + | |||
<math> A = T\widehat{A}T^*, \quad B = T\widehat{B}, \quad C = \widehat{C}T^*, \quad D = 0,</math> |
<math> A = T\widehat{A}T^*, \quad B = T\widehat{B}, \quad C = \widehat{C}T^*, \quad D = 0,</math> |
||
| + | |||
| − | with |
||
| − | <math> T = \left[\begin{array}{ccc} T_0 & & \\ & \ddots & \\ & & T_0 \end{array}\right] </math>, |
+ | with <math> T = \left[\begin{array}{ccc} T_0 & & \\ & \ddots & \\ & & T_0 \end{array}\right] </math>, |
for <math>T_0 = \frac{1}{\sqrt{2}}\left[\begin{array}{cc} 1 & -j\\ 1 & j \end{array}\right]</math>. |
for <math>T_0 = \frac{1}{\sqrt{2}}\left[\begin{array}{cc} 1 & -j\\ 1 & j \end{array}\right]</math>. |
||
Revision as of 13:50, 28 November 2011
Introduction
On this page you will find a purely synthetic parametric model. The goal is to have a simple parametric model which one can use to experiment with different system orders, parameter values etc.
System description
The parameter  scales the real part of the system poles, that is,
scales the real part of the system poles, that is, 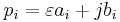 .
For a system in pole-residue form
.
For a system in pole-residue form
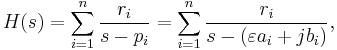
we can then write down the state-space realisation
![\widehat{A} = \varepsilon \left[\begin{array}{ccc} a_1 & & \\ & \ddots & \\ & & a_n\end{array}\right] +\left[\begin{array}{ccc} jb_1 & & \\ & \ddots & \\ & & jb_n\end{array}\right] = \varepsilon \widehat{A}_\varepsilon + \widehat{A}_0,](/morwiki/images/math/1/0/8/10836c8d14a066efc2687e4804a23487.png)
![\widehat{B} = [1,\ldots,1]^T,\quad \widehat{C} = [r_1,\ldots,r_n],\quad D = 0.](/morwiki/images/math/0/1/9/01952f4b905489c1f4686227dc13e409.png)
Notice that the system matrices have complex entries.
For simplicity, assume that  is even,
is even, 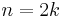 , and that all system poles are complex and ordered in complex conjugate pairs, i.e.
, and that all system poles are complex and ordered in complex conjugate pairs, i.e.
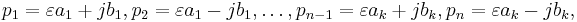
which also implies that the residues form complex conjugate pairs 
Then a realization with matrices having real entries is given by
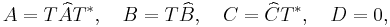
with ![T = \left[\begin{array}{ccc} T_0 & & \\ & \ddots & \\ & & T_0 \end{array}\right]](/morwiki/images/math/d/c/3/dc37eb655d2a4067275e0bda69bd1dba.png) ,
for
,
for ![T_0 = \frac{1}{\sqrt{2}}\left[\begin{array}{cc} 1 & -j\\ 1 & j \end{array}\right]](/morwiki/images/math/8/5/e/85e1ad121c593170f5387aaed11595c6.png) .
.
