m (Start of the page) |
|||
| Line 4: | Line 4: | ||
| − | A stable system <math> |
+ | A stable system <math>\Sigma</math> , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations |
<math> AP+PA^T+BB^T=0,\quad A^TQ+QA+C^TC=0</math> |
<math> AP+PA^T+BB^T=0,\quad A^TQ+QA+C^TC=0</math> |
||
| Line 10: | Line 10: | ||
satisfy <math> P=Q=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n\geq0</math> |
satisfy <math> P=Q=diag(\sigma_1,\dots,\sigma_n)</math> with <math> \sigma_1\geq\sigma_2\geq \dots\geq\sigma_n\geq0</math> |
||
| + | |||
| + | The spectrum of <math> (PQ)^{\frac{1}{2}}</math> which is <math>\{\sigma_1,\dots,\sigma_n\}</math> are the Hankel singular values. |
||
==References== |
==References== |
||
Revision as of 09:47, 25 March 2013
An important projection model reduction method which delivers high quality reduced models by making an extra effort in choosing the projection subspaces.
A stable system 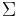 , realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations
, realized by (A,B,C,D) is called balanced, if the Gramians, i.e. the solutions P,Q of the Lyapunov equations
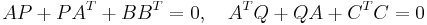
satisfy 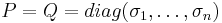 with
with 
The spectrum of 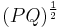 which is
which is  are the Hankel singular values.
are the Hankel singular values.
