Sound transmission through a plate

Note: This page has not been verified by our editors.

Sound Transmission through a Plate

Background
Benchmark ID	soundTransmission_n95480m1q1
Category	misc
System-Class	LTI-SOS
Parameters
nstates	95480
ninputs	1
noutputs	1
nparameters	0
components	B, C, E, K, M
Copyright
License	Creative Commons Attribution 4.0 International
Creator	Quirin Aumann
Editor	Quirin Aumann
Location
https://zenodo.org/record/7670587/files/soundTransmission_n95480m1q1.mat

Figure 1: Sketch of the geometry.

Figure 2: Transfer function.

Description

The Sound transmission through a plate benchmark models the radiation of a vibrating plate and the excitation of a structure by an oscillating acoustic fluid. It is based on an experiment by Guy.

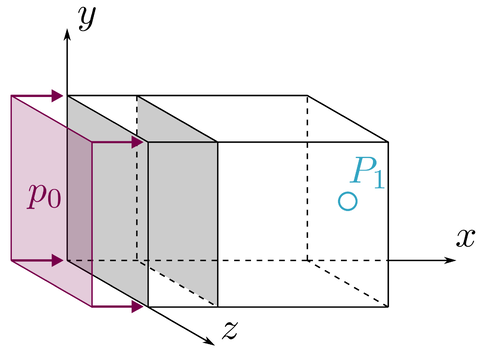
The system consists of a cuboid acoustic cavity, where one wall is considered a system of two parallel elastic brass plates with a \(2\,\mathrm{cm}\) air gap between them; all other walls are considered rigid. The plates measure \(0.2 \times 0.2\,\mathrm{m}\) and have a thickness of \(t = 0.9144\,\mathrm{mm}\); the receiving cavity is \(0.2\,\mathrm{m}\) wide. The outer plate is excited by a uniform pressure load and the resulting acoustic pressure in the receiving cavity is measured at the middle of the rigid wall opposite to the elastic plate (\(P_1\) in the sketch).

The following material parameters have been considered for the brass plates and the acoustic fluid:

Part	Parameter	Value	Unit
Brass plates	\(E\)	\(104\)	\(\mathrm{GPa}\)
	\(\rho\)	\(8500\)	\(\mathrm{kg}\,\mathrm{m}^{-3}\)
	\(\nu\)	\(0.37\)	\(-\)
Acoustic fluid	\(c\)	\(343\)	\(\mathrm{m}\,\mathrm{s}^{-1}\)
	\( \rho\)	\( 1.21\)	\( \mathrm{kg}\,\mathrm{m}^{-3}\)

Dimensions

System structure:

\[ \begin{align} M \ddot{x}(t) + E \dot{x}(t) + K x(t) &= B u(t), \\ y(t) &= C x(t) \end{align} \]

System dimensions\[M \in \mathbb{R}^{n \times n}\], \(E \in \mathbb{R}^{n \times n}\), \(K \in \mathbb{R}^{n \times n}\), \(B \in \mathbb{R}^{n \times 1}\), \(C \in \mathbb{R}^{1 \times n}\), with \(n=95\,480\).

Proportional damping, i.e. \(E=\alpha M + \beta K\), with \(\alpha=0, \beta=1\cdot 10^{-7}\) is considered. The two-way coupling between the structure and the acoustic fluid results in non-symmetric matrices \(M, E, K\).

Data

The data is available at Zenodo.

Remarks

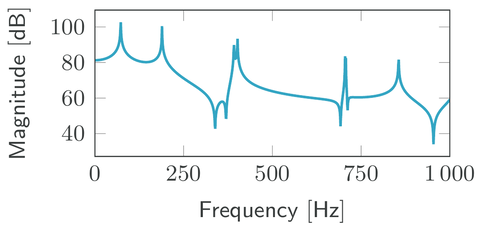
• The numerical model resembles the experimental data in a frequency range from \(1\,\mathrm{Hz}\) to \(1000\,\mathrm{Hz}\). The frequency response in this range is also included in the dataset.
• The finite element discretization has been performed with Kratos Multiphysics.
• The system has unstable eigenvalues. This is common in interior acoustic problems where no damping is assumed for the acoustic fluid.
• A comparison of different interpolation-based MOR methods using this benchmark example is available in

Citation

To cite this benchmark, use the following references:

• For the benchmark itself and its data:

 @Misc{dataAum22,
   author =       {Aumann, Q.},
   title =        {Matrices for a sound transmission problem},
   howpublished = {hosted at {MORwiki} -- Model Order Reduction Wiki},
   year =         2022,
   doi =          {10.5281/zenodo.7300346}
 }

• For the background on the benchmark:

 @Article{AumW23,
   author =       {Aumann, Q. and Werner, S.~W.~R.},
   title =        {Structured model order reduction for vibro-acoustic problems using interpolation and balancing methods},
   journal =      {Journal of Sound and Vibration},
   volume =       543,
   year =         2023,
   pages =        {117363},
   doi =          {10.1016/j.jsv.2022.117363},
   publisher =    {Elsevier {BV}}
 }