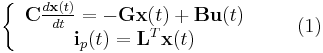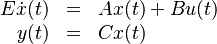| Background | |
|---|---|
| Benchmark ID |
|
| Category |
misc |
| System-Class |
LTI-FOS |
| Parameters | |
| nstates |
|
| ninputs |
|
| noutputs |
|
| nparameters |
0 |
| components |
A, B, C, E |
| Copyright | |
| License |
NA |
| Creator | |
| Editor | |
| Location | |
|
NA | |
Definition
In communications and electronic engineering, a transmission line is a specialized cable designed to carry alternating current of radio frequency, that is, currents with a frequency high enough that their wave nature must be taken into account. Transmission lines are used for purposes such as connecting radio transmitters and receivers with their antennas, distributing cable television signals, and computer network connections.
In many electric circuits, the length of the wires connecting the components can often be ignored. That is, the voltage on the wire at a given time can be assumed to be the same at all points. However, when the voltage changes as fast as the signal travels through the wire, the length becomes important and the wire must be treated as a transmission line, with distributed parameters. Stated in another way, the length of the wire is important when the signal includes frequency components with corresponding wavelengths comparable to or less than the length of the wire.
A common rule of thumb is that the cable or wire should be treated as a transmission line if its length is greater than 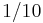 of the wavelength,
and the interconnect is called "electrically long".
At this length the phase delay and the interference of any reflections on the line (as well as other undesired effects) become important and can lead to unpredictable behavior in systems which have not been carefully designed using transmission line theory.
of the wavelength,
and the interconnect is called "electrically long".
At this length the phase delay and the interference of any reflections on the line (as well as other undesired effects) become important and can lead to unpredictable behavior in systems which have not been carefully designed using transmission line theory.
Description
The decrease of integrated circuit feature size and the increase of operating frequencies require 3-D electromagnetic methods, such as the Partial Element Equivalent Circuit (PEEC) method; it stems from the integral equation form of Maxwell's equations. The main difference of the PEEC method with other integral-Equation-based techniques, such as the method of moments, resides in the fact that it provides a circuit interpretation of the Electric Field Integral Equation (EFIE) in terms of partial elements, namely resistances, partial inductances, and coefficients of potential. In the standard approach, volumes and surfaces are discretized into elementary regions, hexahedra, and patches respectively over which the current and charge densities are expanded into a series of basis functions. Pulse basis functions are usually adopted as expansion and weight functions. Such choice of pulse basis functions corresponds to assuming constant current density and charge density over the elementary volume (inductive) and surface (capacitive) cells, respectively. Following the standard Galerkin's testing procedure, topological elements, namely nodes and branches, are generated and electrical lumped elements are identified modeling both the magnetic and electric field coupling. Conductors are modeled by their ohmic resistance, while dielectrics requires modeling the excess charge due to the dielectric polarization. Magnetic and electric field coupling are modeled by partial inductances and coefficients of potential, respectively.
The magnetic field coupling between two inductive volume cells 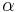 and
and 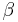 is described by the partial inductance
is described by the partial inductance
where 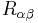 is the distance between any two points in the volumes
is the distance between any two points in the volumes 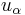 and
and 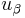 with
with 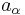 and
and 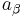 their cross section. The electric field coupling between two capacitive surface cells
their cross section. The electric field coupling between two capacitive surface cells 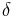 and
and 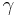 is modeled by the coefficient of the potential
is modeled by the coefficient of the potential
where 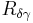 is the distance between any two points on the surfaces
is the distance between any two points on the surfaces 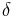 and
and 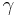 , while
, while 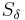 and
and 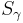 denote the area of their respective surfaces [1].
denote the area of their respective surfaces [1].
Generalized Kirchhoff's laws for conductors, when dielectrics are considered, can be rewritten as
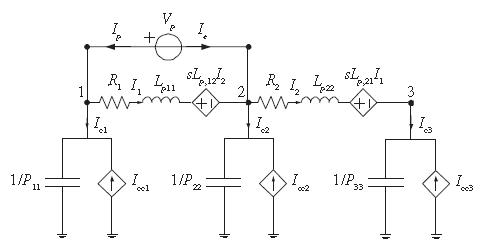
where 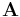 is the connectivity matrix,
is the connectivity matrix, 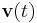 denotes the node potentials to infinity,
denotes the node potentials to infinity, 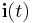 and
and 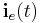 represent the currents flowing in volume cells and the external currents, respectively,
represent the currents flowing in volume cells and the external currents, respectively, 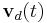 is the excess capacitance voltage drop, which is related to the excess charge by
is the excess capacitance voltage drop, which is related to the excess charge by 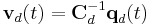 . A selection matrix
. A selection matrix 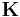 is introduced to define the port voltages by selecting node potentials. The same matrix is used to obtain the external currents
is introduced to define the port voltages by selecting node potentials. The same matrix is used to obtain the external currents 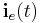 by the currents
by the currents 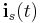 , which are of opposite sign with respect to the
, which are of opposite sign with respect to the  port currents
port currents 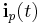 ,
,
An example of PEEC circuit electrical quantities for a conductor elementary cell is illustrated, in the Laplace domain, in Fig. 1, where the current-controlled voltage sources 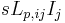 and the current-controlled current sources
and the current-controlled current sources 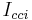 model the magnetic and electric coupling, respectively.
model the magnetic and electric coupling, respectively.
Thus, assuming that we are interested in generating an admittance representation having 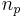 output currents under voltage excitation, and let us denote with
output currents under voltage excitation, and let us denote with 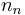 the number of nodes,
the number of nodes, 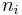 the number of branches where currents flow,
the number of branches where currents flow, 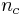 the number of branches of conductors,
the number of branches of conductors, 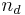 the number of dielectrics,
the number of dielectrics, 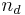 the additional unknowns since dielectrics require the excess capacitance to model the polarization charge, and
the additional unknowns since dielectrics require the excess capacitance to model the polarization charge, and 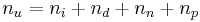 the global number of unknowns, and if the Modified Nodal Analysis (MNA) approach is used, we have:
the global number of unknowns, and if the Modified Nodal Analysis (MNA) approach is used, we have:
Here 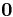 is a matrix of zeros,
is a matrix of zeros, 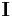 is the identity matrix, both are with appropriate dimensions, and
is the identity matrix, both are with appropriate dimensions, and ![\Phi=\left[ \begin{array}{c} \textbf{0}_{n_c,n_d} \\ \textbf{I}_{n_d,n_d} \end{array}\right]](/morwiki/images/math/d/c/d/dcdd5e7b53a7fabe1acadab76266f310.png) . Then, in a more compact form, the above equation can be written as:
. Then, in a more compact form, the above equation can be written as:
with ![\textbf{x}(t)=\left[ \begin{array}{cccc} \textbf{q}(t)\quad\textbf{i}(t)\quad\textbf{v}_d(t)\quad\textbf{i}_s(t) \end{array}\right]^T](/morwiki/images/math/1/d/f/1df329a936daa3df58aa5b0215229604.png) . Since this is an
. Since this is an 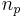 -port formulation, whereby the only sources are the voltage sources at the
-port formulation, whereby the only sources are the voltage sources at the 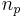 -ports nodes,
-ports nodes, 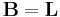 where
where 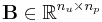 (for more details on this model, refer to [1]).
(for more details on this model, refer to [1]).
Motivation of MOR
Since the number of equations produced by 3-D electromagnetic method PEEC is usually very large, the inclusion of the PEEC model directly into a circuit simulator (like SPICE) is computationally intractable for complex structures, where the number of circuit elements can be tens of thousands.
Data
All data sets (in a MATLAB formatted data, downloadable in TransmissionLines.rar) in Fig. 1 are referred to as the multiconductor transmission lines in a MNA form, coming from the PEEC method (then, with dense matrices since they are obtained from the integral formulation of Maxwell's equation).
The LTI descriptor systems have the form of, equation 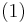 , where
, where 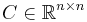 (with
(with 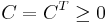 ),
), 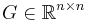 (with
(with 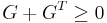 ),
), 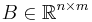 and
and 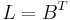 ,
, 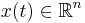 is the vector of variables (charges, currents and node potential), the input signal
is the vector of variables (charges, currents and node potential), the input signal 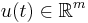 are the sources (current or voltage generators depending on what one wants to analyze:
the impedances or the admittances) linked to some node, the output
are the sources (current or voltage generators depending on what one wants to analyze:
the impedances or the admittances) linked to some node, the output 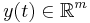 are the observation across the node where the sources are inserted. An accurate model of the dynamics of these data sets is generated between 10 kHz and 20 GHz.
are the observation across the node where the sources are inserted. An accurate model of the dynamics of these data sets is generated between 10 kHz and 20 GHz.
| Name of the data set | Matrices | Dimension | Number of inputs |
|---|---|---|---|
| dsysPEEC-MTLn1600m14 | 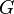 , ,  , ,  ( (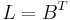 ) ) |
1600 | 14 |
| dsysPEEC-MTLn2624m30 | dss object (*) | 2624 | 30 |
| dsysPEEC-MTLn5248m62 | dss object (*) | 5248 | 62 |
one can extract the matrices with Matlab command:
[G,B,L,D,C] = dssdata(dssObjectName);
e.g., if one wants to work on one of the last two data sets of this table,
just load it into the Matlab Workspace and type the command aforementioned on the Command Windows;
for the first example, once one loads the data, the Workspace shows directly the matrices.
Note that 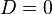 .
.
Dimensions
System structure:
System dimensions:
 ,
,
 ,
,
 ,
,
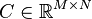 .
.
System variants:
dsysPEEC-MTLn1600m14: 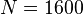 ,
, 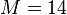 ,
dsysPEEC-MTLn2624m30:
,
dsysPEEC-MTLn2624m30: 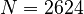 ,
, 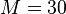 ,
dsysPEEC-MTLn5248m62:
,
dsysPEEC-MTLn5248m62: 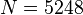 ,
, 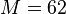
References
- ↑ 1.0 1.1 1.2 F. Ferranti, G. Antonini, T. Dhaene, L. Knockaert, and A. E. Ruehli, "Physics-based passivity-preserving parameterized model order reduction for PEEC circuit analysis", IEEE Transactions on Components, Packaging and Manufacturing Technology, 1(3): 399--409, 2011.

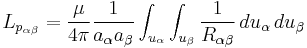
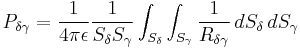
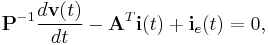
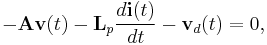
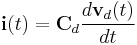
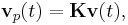
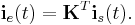
![\left[ \begin{array}{cccc} \textbf{P} & \textbf{0}_{n_n,n_i} & \textbf{0}_{n_n,n_d} & \textbf{0}_{n_n,n_p} \\ \textbf{0}_{n_i,n_n} & \textbf{L}_p & \textbf{0}_{n_i,n_d} & \textbf{0}_{n_i,n_p} \\ \textbf{0}_{n_d,n_n} & \textbf{0}_{n_d,n_i} & \textbf{C}_d & \textbf{0}_{n_d,n_p} \\ \textbf{0}_{n_p,n_n} & \textbf{0}_{n_p,n_i} & \textbf{0}_{n_p,n_d} & \textbf{0}_{n_p,n_p} \end{array}\right]\frac{d}{dt}\left[ \begin{array}{c}\textbf{q}(t) \\ \textbf{i}(t) \\ \textbf{v}_d(t) \\ \textbf{i}_s(t) \end{array}\right]=](/morwiki/images/math/8/c/9/8c9cf222ccff77533acc740ce2f6176d.png)
![= - \left[ \begin{array}{cccc}\textbf{0}_{n_n,n_n} & -\textbf{P}\textbf{A}^T & \textbf{0}_{n_n,n_d} & \textbf{P}\textbf{K}^T \\ \textbf{AP} & \textbf{R} & \Phi & \textbf{0}_{n_i,n_p} \\ \textbf{0}_{n_d,n_n} & -\Phi^T & \textbf{0}_{n_d,n_d} & \textbf{0}_{n_d,n_p} \\ -\textbf{K}\textbf{P} & \textbf{0}_{n_p,n_i} & \textbf{0}_{n_p,n_d} & \textbf{0}_{n_p,n_p} \end{array}\right]\cdot\left[ \begin{array}{c} \textbf{q}(t) \\ \textbf{i}(t) \\ \textbf{v}_d(t) \\ \textbf{i}_s(t) \end{array}\right]+ \left[ \begin{array}{c}\textbf{0}_{n_n+n_i+n_d,n_p} \\ -\textbf{I}_{n_p,n_p} \end{array}\right] \cdot [ \textbf{v}_p(t) ].](/morwiki/images/math/5/3/c/53ce979cca87aa9611b60505e409810c.png)